Deep connections between learning from limited labels & physical parameter estimation -- inspiration for regularization
Paper and Code
Mar 17, 2020
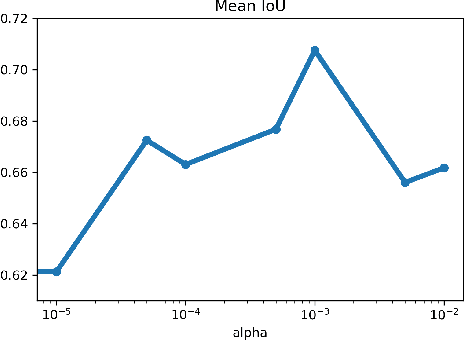
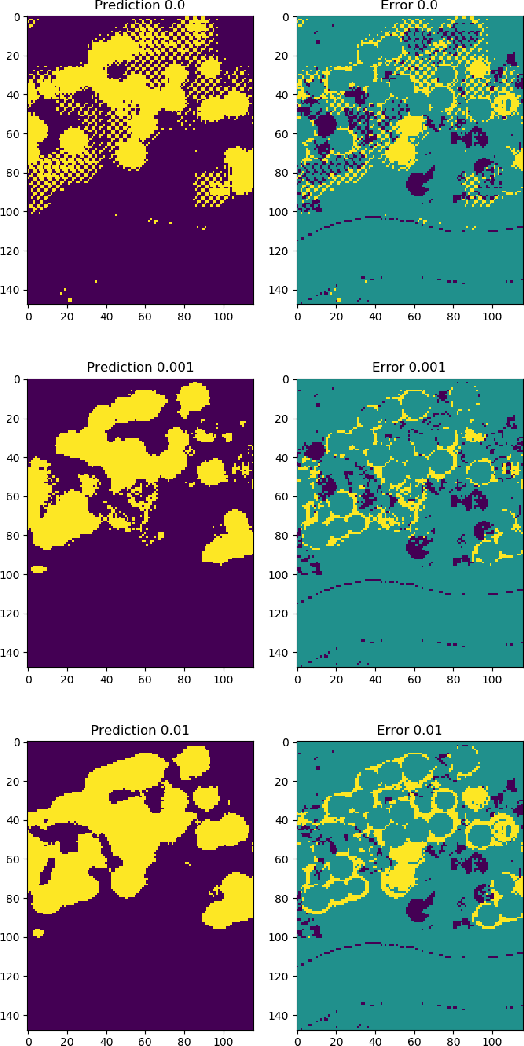
Recently established equivalences between differential equations and the structure of neural networks enabled some interpretation of training of a neural network as partial-differential-equation (PDE) constrained optimization. We add to the previously established connections, explicit regularization that is particularly beneficial in the case of single large-scale examples with partial annotation. We show that explicit regularization of model parameters in PDE constrained optimization translates to regularization of the network output. Examination of the structure of the corresponding Lagrangian and backpropagation algorithm do not reveal additional computational challenges. A hyperspectral imaging example shows that minimum prior information together with cross-validation for optimal regularization parameters boosts the segmentation accuracy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge