Deep Residual Echo State Networks: exploring residual orthogonal connections in untrained Recurrent Neural Networks

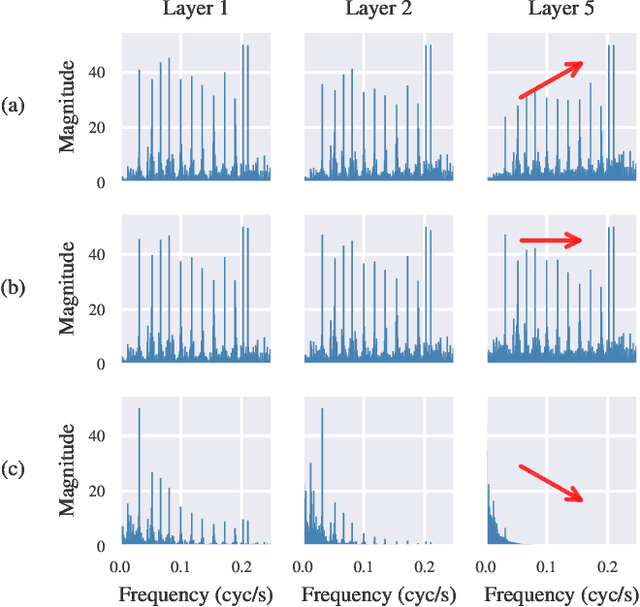
Echo State Networks (ESNs) are a particular type of untrained Recurrent Neural Networks (RNNs) within the Reservoir Computing (RC) framework, popular for their fast and efficient learning. However, traditional ESNs often struggle with long-term information processing. In this paper, we introduce a novel class of deep untrained RNNs based on temporal residual connections, called Deep Residual Echo State Networks (DeepResESNs). We show that leveraging a hierarchy of untrained residual recurrent layers significantly boosts memory capacity and long-term temporal modeling. For the temporal residual connections, we consider different orthogonal configurations, including randomly generated and fixed-structure configurations, and we study their effect on network dynamics. A thorough mathematical analysis outlines necessary and sufficient conditions to ensure stable dynamics within DeepResESN. Our experiments on a variety of time series tasks showcase the advantages of the proposed approach over traditional shallow and deep RC.

Residual Reservoir Memory Networks

We introduce a novel class of untrained Recurrent Neural Networks (RNNs) within the Reservoir Computing (RC) paradigm, called Residual Reservoir Memory Networks (ResRMNs). ResRMN combines a linear memory reservoir with a non-linear reservoir, where the latter is based on residual orthogonal connections along the temporal dimension for enhanced long-term propagation of the input. The resulting reservoir state dynamics are studied through the lens of linear stability analysis, and we investigate diverse configurations for the temporal residual connections. The proposed approach is empirically assessed on time-series and pixel-level 1-D classification tasks. Our experimental results highlight the advantages of the proposed approach over other conventional RC models.

Message-Passing State-Space Models: Improving Graph Learning with Modern Sequence Modeling

The recent success of State-Space Models (SSMs) in sequence modeling has motivated their adaptation to graph learning, giving rise to Graph State-Space Models (GSSMs). However, existing GSSMs operate by applying SSM modules to sequences extracted from graphs, often compromising core properties such as permutation equivariance, message-passing compatibility, and computational efficiency. In this paper, we introduce a new perspective by embedding the key principles of modern SSM computation directly into the Message-Passing Neural Network framework, resulting in a unified methodology for both static and temporal graphs. Our approach, MP-SSM, enables efficient, permutation-equivariant, and long-range information propagation while preserving the architectural simplicity of message passing. Crucially, MP-SSM enables an exact sensitivity analysis, which we use to theoretically characterize information flow and evaluate issues like vanishing gradients and over-squashing in the deep regime. Furthermore, our design choices allow for a highly optimized parallel implementation akin to modern SSMs. We validate MP-SSM across a wide range of tasks, including node classification, graph property prediction, long-range benchmarks, and spatiotemporal forecasting, demonstrating both its versatility and strong empirical performance.

Transitions in echo index and dependence on input repetitions

The echo index counts the number of simultaneously stable asymptotic responses of a nonautonomous (i.e. input-driven) dynamical system. It generalizes the well-known echo state property for recurrent neural networks - this corresponds to the echo index being equal to one. In this paper, we investigate how the echo index depends on parameters that govern typical responses to a finite-state ergodic external input that forces the dynamics. We consider the echo index for a nonautonomous system that switches between a finite set of maps, where we assume that each map possesses a finite set of hyperbolic equilibrium attractors. We find the minimum and maximum repetitions of each map are crucial for the resulting echo index. Casting our theoretical findings in the RNN computing framework, we obtain that for small amplitude forcing the echo index corresponds to the number of attractors for the input-free system, while for large amplitude forcing, the echo index reduces to one. The intermediate regime is the most interesting; in this region the echo index depends not just on the amplitude of forcing but also on more subtle properties of the input.

Edge of stability echo state networks

In this paper, we propose a new Reservoir Computing (RC) architecture, called the Edge of Stability Echo State Network (ES$^2$N). The introduced ES$^2$N model is based on defining the reservoir layer as a convex combination of a nonlinear reservoir (as in the standard ESN), and a linear reservoir that implements an orthogonal transformation. We provide a thorough mathematical analysis of the introduced model, proving that the whole eigenspectrum of the Jacobian of the ES2N map can be contained in an annular neighbourhood of a complex circle of controllable radius, and exploit this property to demonstrate that the ES$^2$N's forward dynamics evolves close to the edge-of-chaos regime by design. Remarkably, our experimental analysis shows that the newly introduced reservoir model is able to reach the theoretical maximum short-term memory capacity. At the same time, in comparison to standard ESN, ES$^2$N is shown to offer a favorable trade-off between memory and nonlinearity, as well as a significant improvement of performance in autoregressive nonlinear modeling.

Random orthogonal additive filters: a solution to the vanishing/exploding gradient of deep neural networks

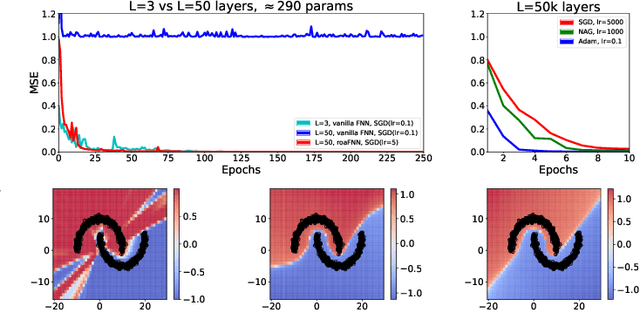
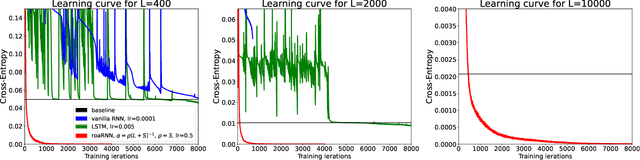
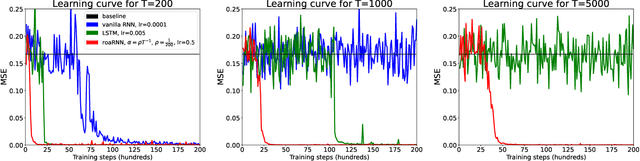
Since the recognition in the early nineties of the vanishing/exploding (V/E) gradient issue plaguing the training of neural networks (NNs), significant efforts have been exerted to overcome this obstacle. However, a clear solution to the V/E issue remained elusive so far. In this manuscript a new architecture of NN is proposed, designed to mathematically prevent the V/E issue to occur. The pursuit of approximate dynamical isometry, i.e. parameter configurations where the singular values of the input-output Jacobian are tightly distributed around 1, leads to the derivation of a NN's architecture that shares common traits with the popular Residual Network model. Instead of skipping connections between layers, the idea is to filter the previous activations orthogonally and add them to the nonlinear activations of the next layer, realising a convex combination between them. Remarkably, the impossibility for the gradient updates to either vanish or explode is demonstrated with analytical bounds that hold even in the infinite depth case. The effectiveness of this method is empirically proved by means of training via backpropagation an extremely deep multilayer perceptron of 50k layers, and an Elman NN to learn long-term dependencies in the input of 10k time steps in the past. Compared with other architectures specifically devised to deal with the V/E problem, e.g. LSTMs for recurrent NNs, the proposed model is way simpler yet more effective. Surprisingly, a single layer vanilla RNN can be enhanced to reach state of the art performance, while converging super fast; for instance on the psMNIST task, it is possible to get test accuracy of over 94% in the first epoch, and over 98% after just 10 epochs.

Interpreting RNN behaviour via excitable network attractors

Machine learning has become a basic tool in scientific research and for the development of technologies with significant impact on society. In fact, such methods allow to discover regularities in data and make predictions without explicit knowledge of the rules governing the system under analysis. However, a price must be paid for exploiting such a modeling flexibility: machine learning methods are usually black-box, meaning that it is difficult to fully understand what the machine is doing and how. This poses constraints on the applicability of such methods, neglecting the possibility to gather novel scientific insights from experimental data. Our research aims to open the black-box of recurrent neural networks, an important family of neural networks suitable to process sequential data. Here, we propose a novel methodology that allows to provide a mechanistic interpretation of their behaviour when used to solve computational tasks. The methodology is based on mathematical constructs called excitable network attractors, which are models represented as networks in phase space composed by stable attractors and excitable connections between them. As the behaviour of recurrent neural networks depends on training and inputs driving the autonomous system, we introduce an algorithm to extract network attractors directly from a trajectory generated by the neural network while solving tasks. Simulations conducted on a controlled benchmark highlight the relevance of the proposed methodology for interpreting the behaviour of recurrent neural networks on tasks that involve learning a finite number of stable states.