On expected signatures and signature cumulants in semimartingale models

The concept of signatures and expected signatures is vital in data science, especially for sequential data analysis. The signature transform, a Cartan type development, translates paths into high-dimensional feature vectors, capturing their intrinsic characteristics. Under natural conditions, the expectation of the signature determines the law of the signature, providing a statistical summary of the data distribution. This property facilitates robust modeling and inference in machine learning and stochastic processes. Building on previous work by the present authors [Unified signature cumulants and generalized Magnus expansions, FoM Sigma '22] we here revisit the actual computation of expected signatures, in a general semimartingale setting. Several new formulae are given. A log-transform of (expected) signatures leads to log-signatures (signature cumulants), offering a significant reduction in complexity.

Stability of Deep Neural Networks via discrete rough paths

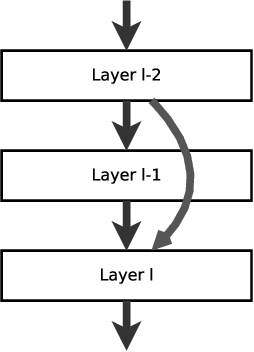
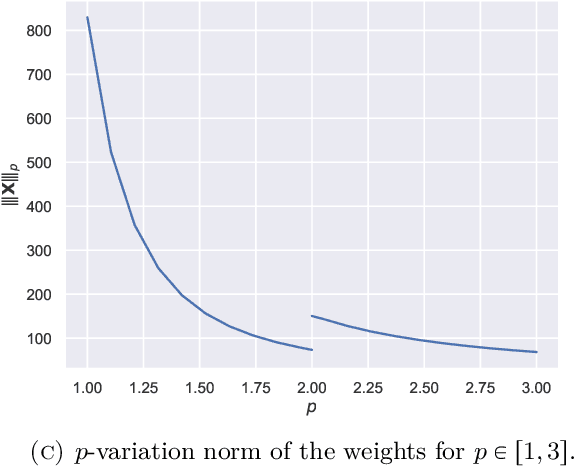
Using rough path techniques, we provide a priori estimates for the output of Deep Residual Neural Networks in terms of both the input data and the (trained) network weights. As trained network weights are typically very rough when seen as functions of the layer, we propose to derive stability bounds in terms of the total $p$-variation of trained weights for any $p\in[1,3]$. Unlike the $C^1$-theory underlying the neural ODE literature, our estimates remain bounded even in the limiting case of weights behaving like Brownian motions, as suggested in [arXiv:2105.12245]. Mathematically, we interpret residual neural network as solutions to (rough) difference equations, and analyse them based on recent results of discrete time signatures and rough path theory.

Generalized iterated-sums signatures

We explore the algebraic properties of a generalized version of the iterated-sums signature, inspired by previous work of F.~Kir\'aly and H.~Oberhauser. In particular, we show how to recover the character property of the associated linear map over the tensor algebra by considering a deformed quasi-shuffle product of words on the latter. We introduce three non-linear transformations on iterated-sums signatures, close in spirit to Machine Learning applications, and show some of their properties.

Tropical time series, iterated-sums signatures and quasisymmetric functions

Driven by the need for principled extraction of features from time series,we introduce the iterated-sums signature over any commutative semiring.The case of the tropical semiring is a central, and our motivating, example,as it leads to features of (real-valued) time series that are not easily availableusing existing signature-type objects.

Signatures in Shape Analysis: an Efficient Approach to Motion Identification

Signatures provide a succinct description of certain features of paths in a reparametrization invariant way. We propose a method for classifying shapes based on signatures, and compare it to current approaches based on the SRV transform and dynamic programming.

Time warping invariants of multidimensional time series

In data science, one is often confronted with a time series representing measurements of some quantity of interest. Usually, in a first step, features of the time series need to be extracted. These are numerical quantities that aim to succinctly describe the data and to dampen the influence of noise. In some applications, these features are also required to satisfy some invariance properties. In this paper, we concentrate on time-warping invariants. We show that these correspond to a certain family of iterated sums of the increments of the time series, known as quasisymmetric functions in the mathematics literature. We present these invariant features in an algebraic framework, and we develop some of their basic properties.