On expected signatures and signature cumulants in semimartingale models

The concept of signatures and expected signatures is vital in data science, especially for sequential data analysis. The signature transform, a Cartan type development, translates paths into high-dimensional feature vectors, capturing their intrinsic characteristics. Under natural conditions, the expectation of the signature determines the law of the signature, providing a statistical summary of the data distribution. This property facilitates robust modeling and inference in machine learning and stochastic processes. Building on previous work by the present authors [Unified signature cumulants and generalized Magnus expansions, FoM Sigma '22] we here revisit the actual computation of expected signatures, in a general semimartingale setting. Several new formulae are given. A log-transform of (expected) signatures leads to log-signatures (signature cumulants), offering a significant reduction in complexity.

Stability of Deep Neural Networks via discrete rough paths

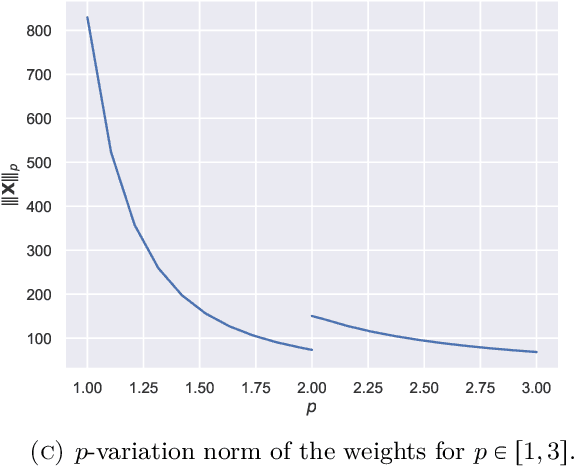
Using rough path techniques, we provide a priori estimates for the output of Deep Residual Neural Networks in terms of both the input data and the (trained) network weights. As trained network weights are typically very rough when seen as functions of the layer, we propose to derive stability bounds in terms of the total $p$-variation of trained weights for any $p\in[1,3]$. Unlike the $C^1$-theory underlying the neural ODE literature, our estimates remain bounded even in the limiting case of weights behaving like Brownian motions, as suggested in [arXiv:2105.12245]. Mathematically, we interpret residual neural network as solutions to (rough) difference equations, and analyse them based on recent results of discrete time signatures and rough path theory.