Accelerating Multiscale Modeling with Hybrid Solvers: Coupling FEM and Neural Operators with Domain Decomposition

Numerical solvers for partial differential equations (PDEs) face challenges balancing computational cost and accuracy, especially in multiscale and dynamic systems. Neural operators can significantly speed up simulations; however, they often face challenges such as error accumulation and limited generalization in multiphysics problems. This work introduces a novel hybrid framework that integrates physics-informed DeepONet with FEM through domain decomposition. The core innovation lies in adaptively coupling FEM and DeepONet subdomains via a Schwarz alternating method. This methodology strategically allocates computationally demanding regions to a pre-trained Deep Operator Network, while the remaining computational domain is solved through FEM. To address dynamic systems, we integrate the Newmark time-stepping scheme directly into the DeepONet, significantly mitigating error accumulation in long-term simulations. Furthermore, an adaptive subdomain evolution enables the ML-resolved region to expand dynamically, capturing emerging fine-scale features without remeshing. The framework's efficacy has been validated across a range of solid mechanics problems, including static, quasi-static, and dynamic regimes, demonstrating accelerated convergence rates (up to 20% improvement compared to FE-FE approaches), while preserving solution fidelity with error < 1%. Our case studies show that our proposed hybrid solver: (1) maintains solution continuity across subdomain interfaces, (2) reduces computational costs by eliminating fine mesh requirements, (3) mitigates error accumulation in time-dependent simulations, and (4) enables automatic adaptation to evolving physical phenomena. This work bridges the gap between numerical methods and AI-driven surrogates, offering a scalable pathway for high-fidelity simulations in engineering and scientific applications.

Precision Glass Thermoforming Assisted by Neural Networks

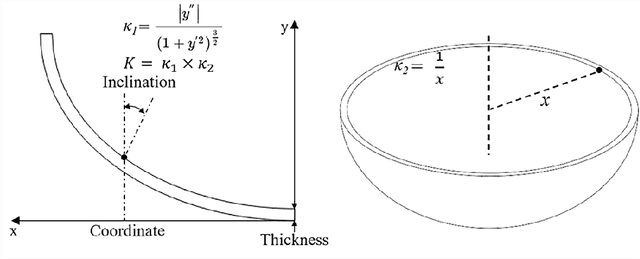
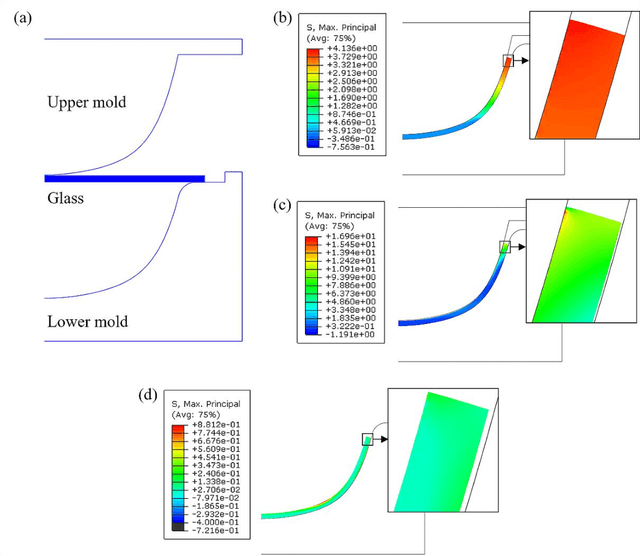
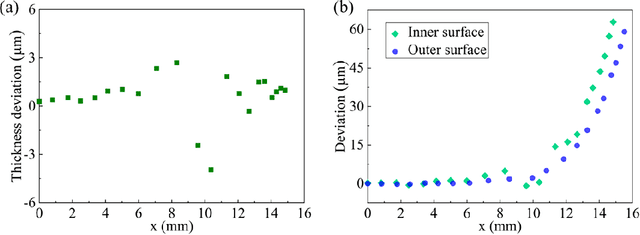
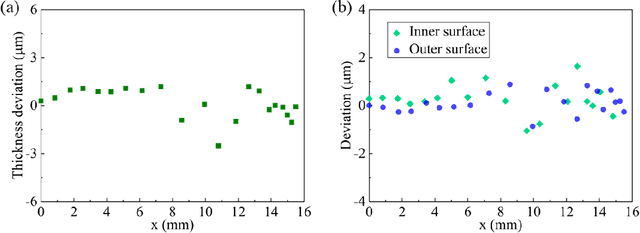
Glass with good processability, chemical inertness, and optical transparency has been widely used in optical and aesthetic products, many of which require curve pro-files with high precision. To meet the increasingly tightened geometrical tolerances and fast product updating rates, the traditional approach of developing a thermoform-ing process through trials and errors can cause a large waste of time and resources and often end up with failure. Hence, there is a need to develop an efficient predictive model, replacing the costly simulations or experiments, to assist the design of preci-sion glass thermoforming. In this work, we report a dimensionless back-propagation neural network (BPNN) that can adequately predict the form errors and thus compen-sate for these errors in mold design to achieve precision glass molding. Based on the precision molds, also discussed is the issue of error magnification considering that cover glass for AR/VR glasses or smartphones, with extremely large scale of produc-tion, may require a lower level of mold machining accuracy. It is expected that this BPNN will also be implementable in the glass-manufacturing industry, i.e., trained using industrial data for precision mold designs.