Learning Hidden Physics and System Parameters with Deep Operator Networks

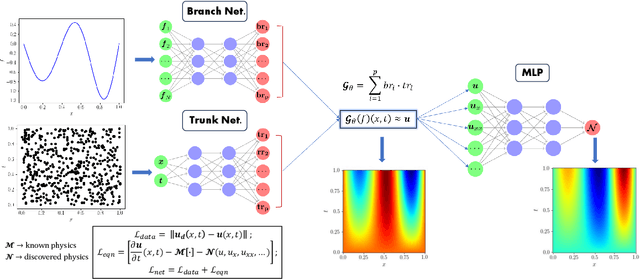
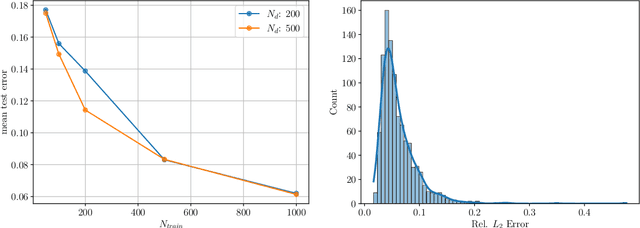
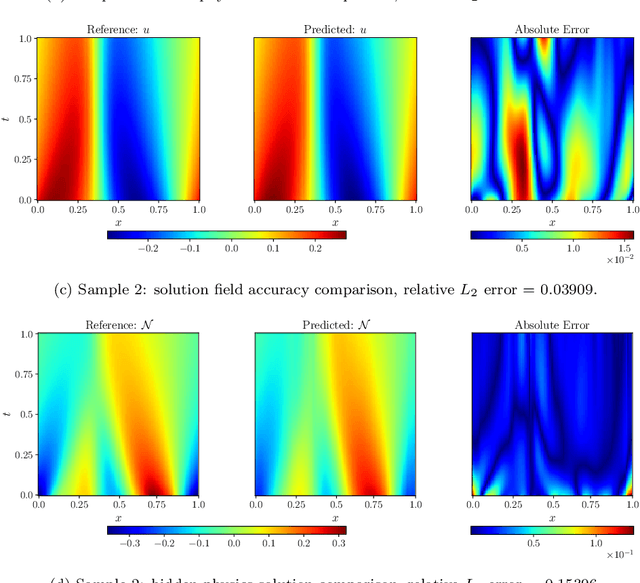
Big data is transforming scientific progress by enabling the discovery of novel models, enhancing existing frameworks, and facilitating precise uncertainty quantification, while advancements in scientific machine learning complement this by providing powerful tools to solve inverse problems to identify the complex systems where traditional methods falter due to sparse or noisy data. We introduce two innovative neural operator frameworks tailored for discovering hidden physics and identifying unknown system parameters from sparse measurements. The first framework integrates a popular neural operator, DeepONet, and a physics-informed neural network to capture the relationship between sparse data and the underlying physics, enabling the accurate discovery of a family of governing equations. The second framework focuses on system parameter identification, leveraging a DeepONet pre-trained on sparse sensor measurements to initialize a physics-constrained inverse model. Both frameworks excel in handling limited data and preserving physical consistency. Benchmarking on the Burgers' equation and reaction-diffusion system demonstrates state-of-the-art performance, achieving average $L_2$ errors of $\mathcal{O}(10^{-2})$ for hidden physics discovery and absolute errors of $\mathcal{O}(10^{-3})$ for parameter identification. These results underscore the frameworks' robustness, efficiency, and potential for solving complex scientific problems with minimal observational data.

A novel data generation scheme for surrogate modelling with deep operator networks

Operator-based neural network architectures such as DeepONets have emerged as a promising tool for the surrogate modeling of physical systems. In general, towards operator surrogate modeling, the training data is generated by solving the PDEs using techniques such as Finite Element Method (FEM). The computationally intensive nature of data generation is one of the biggest bottleneck in deploying these surrogate models for practical applications. In this study, we propose a novel methodology to alleviate the computational burden associated with training data generation for DeepONets. Unlike existing literature, the proposed framework for data generation does not use any partial differential equation integration strategy, thereby significantly reducing the computational cost associated with generating training dataset for DeepONet. In the proposed strategy, first, the output field is generated randomly, satisfying the boundary conditions using Gaussian Process Regression (GPR). From the output field, the input source field can be calculated easily using finite difference techniques. The proposed methodology can be extended to other operator learning methods, making the approach widely applicable. To validate the proposed approach, we employ the heat equations as the model problem and develop the surrogate model for numerous boundary value problems.

A novel framework for generalization of deep hidden physics models

Modelling of systems where the full system information is unknown is an oft encountered problem for various engineering and industrial applications, as it's either impossible to consider all the complex physics involved or simpler models are considered to keep within the limits of the available resources. Recent advances in greybox modelling like the deep hidden physics models address this space by combining data and physics. However, for most real-life applications, model generalizability is a key issue, as retraining a model for every small change in system inputs and parameters or modification in domain configuration can render the model economically unviable. In this work we present a novel enhancement to the idea of hidden physics models which can generalize for changes in system inputs, parameters and domains. We also show that this approach holds promise in system discovery as well and helps learn the hidden physics for the changed system inputs, parameters and domain configuration.