Sound propagation in realistic interactive 3D scenes with parameterized sources using deep neural operators

We address the challenge of sound propagation simulations in $3$D virtual rooms with moving sources, which have applications in virtual/augmented reality, game audio, and spatial computing. Solutions to the wave equation can describe wave phenomena such as diffraction and interference. However, simulating them using conventional numerical discretization methods with hundreds of source and receiver positions is intractable, making stimulating a sound field with moving sources impractical. To overcome this limitation, we propose using deep operator networks to approximate linear wave-equation operators. This enables the rapid prediction of sound propagation in realistic 3D acoustic scenes with moving sources, achieving millisecond-scale computations. By learning a compact surrogate model, we avoid the offline calculation and storage of impulse responses for all relevant source/listener pairs. Our experiments, including various complex scene geometries, show good agreement with reference solutions, with root mean squared errors ranging from 0.02 Pa to 0.10 Pa. Notably, our method signifies a paradigm shift as no prior machine learning approach has achieved precise predictions of complete wave fields within realistic domains. We anticipate that our findings will drive further exploration of deep neural operator methods, advancing research in immersive user experiences within virtual environments.

Room dimensions and absorption inference from room transfer function via machine learning

The inference of the absorption configuration of an existing room solely using acoustic signals can be challenging. This research presents two methods for estimating the room dimensions and frequency-dependent absorption coefficients using room transfer functions. The first method, a knowledge-based approach, calculates the room dimensions through damped resonant frequencies of the room. The second method, a machine learning approach, employs multi-task convolutional neural networks for inferring the room dimensions and frequency-dependent absorption coefficients of each surface. The study shows that accurate wave-based simulation data can be used to train neural networks for real-world measurements and demonstrates a potential for this algorithm to be used to estimate the boundary input data for room acoustic simulations. The proposed methods can be a valuable tool for room acoustic simulations during acoustic renovation or intervention projects, as they enable to infer the room geometry and absorption conditions with reasonably small data requirements.

Physics-Informed Neural Networks (PINNs) for Sound Field Predictions with Parameterized Sources and Impedance Boundaries

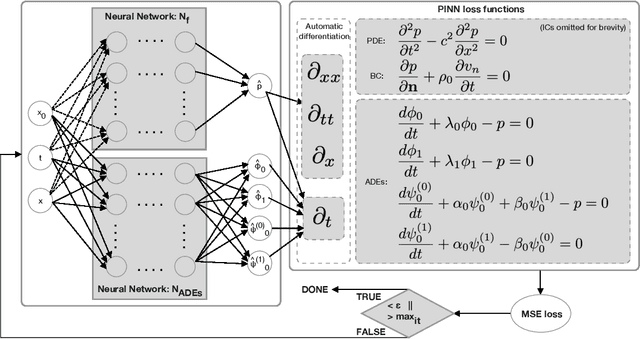
Realistic sound is essential in virtual environments, such as computer games and mixed reality. Efficient and accurate numerical methods for pre-calculating acoustics have been developed over the last decade, however, pre-calculating acoustics makes handling dynamic scenes with moving sources challenging and requires intractable memory storage. A Physics-Informed Neural Networks (PINNS) method is presented, learning a compact and efficient surrogate model with parameterized moving sources and impedance boundaries, satisfying a system of coupled equations. The trained model shows relative mean errors below 2%/0.2 dB, indicating that acoustics with moving sources and impedance boundaries can be predicted in real-time using PINNs.

Efficient numerical room acoustic simulations with parametrized boundaries using the spectral element and reduced basis method

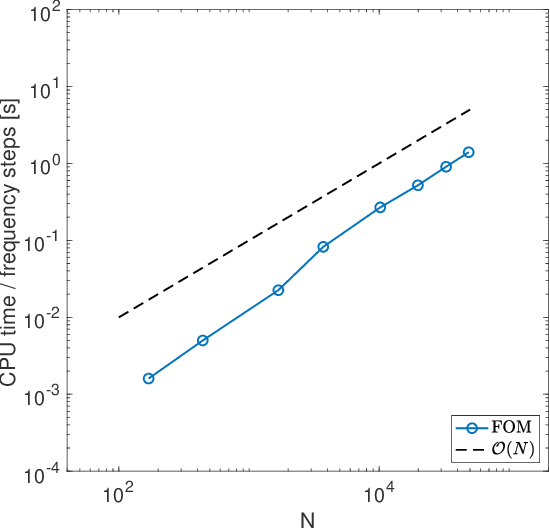
Numerical methods can be used to simulate wave propagation in rooms, with applications in virtual reality and building design. Such methods can be highly accurate but computationally expensive when simulating high frequencies and large domains for long simulation times. Moreover, it is common that solutions are sought for multiple input parameter values, e.g., in design processes in room acoustics, where different boundary absorption properties are evaluated iteratively. We present a framework that combines a spectral element method (SEM) and a reduced basis method (RBM) to achieve a computational cost reduction for parameterized room acoustic simulations. The SEM provides low dispersion and dissipation properties due to the high-order discretization and the RBM reduces the computational burden further when parametrizing the boundary properties for both frequency-independent and dependent conditions. The problem is solved in the Laplace domain, which avoids instability issues on the reduced model. We demonstrate that the use of high-order discretization and model order reduction has significant advantages for room acoustics in terms of computational efficiency and accuracy.