Neural empirical interpolation method for nonlinear model reduction

In this paper, we introduce the neural empirical interpolation method (NEIM), a neural network-based alternative to the discrete empirical interpolation method for reducing the time complexity of computing the nonlinear term in a reduced order model (ROM) for a parameterized nonlinear partial differential equation. NEIM is a greedy algorithm which accomplishes this reduction by approximating an affine decomposition of the nonlinear term of the ROM, where the vector terms of the expansion are given by neural networks depending on the ROM solution, and the coefficients are given by an interpolation of some "optimal" coefficients. Because NEIM is based on a greedy strategy, we are able to provide a basic error analysis to investigate its performance. NEIM has the advantages of being easy to implement in models with automatic differentiation, of being a nonlinear projection of the ROM nonlinearity, of being efficient for both nonlocal and local nonlinearities, and of relying solely on data and not the explicit form of the ROM nonlinearity. We demonstrate the effectiveness of the methodology on solution-dependent and solution-independent nonlinearities, a nonlinear elliptic problem, and a nonlinear parabolic model of liquid crystals.

GFN: A graph feedforward network for resolution-invariant reduced operator learning in multifidelity applications

This work presents a novel resolution-invariant model order reduction strategy for multifidelity applications. We base our architecture on a novel neural network layer developed in this work, the graph feedforward network, which extends the concept of feedforward networks to graph-structured data by creating a direct link between the weights of a neural network and the nodes of a mesh, enhancing the interpretability of the network. We exploit the method's capability of training and testing on different mesh sizes in an autoencoder-based reduction strategy for parametrised partial differential equations. We show that this extension comes with provable guarantees on the performance via error bounds. The capabilities of the proposed methodology are tested on three challenging benchmarks, including advection-dominated phenomena and problems with a high-dimensional parameter space. The method results in a more lightweight and highly flexible strategy when compared to state-of-the-art models, while showing excellent generalisation performance in both single fidelity and multifidelity scenarios.

Machine learning enhanced real-time aerodynamic forces prediction based on sparse pressure sensor inputs

Accurate prediction of aerodynamic forces in real-time is crucial for autonomous navigation of unmanned aerial vehicles (UAVs). This paper presents a data-driven aerodynamic force prediction model based on a small number of pressure sensors located on the surface of UAV. The model is built on a linear term that can make a reasonably accurate prediction and a nonlinear correction for accuracy improvement. The linear term is based on a reduced basis reconstruction of the surface pressure distribution, where the basis is extracted from numerical simulation data and the basis coefficients are determined by solving linear pressure reconstruction equations at a set of sensor locations. Sensor placement is optimized using the discrete empirical interpolation method (DEIM). Aerodynamic forces are computed by integrating the reconstructed surface pressure distribution. The nonlinear term is an artificial neural network (NN) that is trained to bridge the gap between the ground truth and the DEIM prediction, especially in the scenario where the DEIM model is constructed from simulation data with limited fidelity. A large network is not necessary for accurate correction as the linear model already captures the main dynamics of the surface pressure field, thus yielding an efficient DEIM+NN aerodynamic force prediction model. The model is tested on numerical and experimental dynamic stall data of a 2D NACA0015 airfoil, and numerical simulation data of dynamic stall of a 3D drone. Numerical results demonstrate that the machine learning enhanced model can make fast and accurate predictions of aerodynamic forces using only a few pressure sensors, even for the NACA0015 case in which the simulations do not agree well with the wind tunnel experiments. Furthermore, the model is robust to noise.

A graph convolutional autoencoder approach to model order reduction for parametrized PDEs

The present work proposes a framework for nonlinear model order reduction based on a Graph Convolutional Autoencoder (GCA-ROM). In the reduced order modeling (ROM) context, one is interested in obtaining real-time and many-query evaluations of parametric Partial Differential Equations (PDEs). Linear techniques such as Proper Orthogonal Decomposition (POD) and Greedy algorithms have been analyzed thoroughly, but they are more suitable when dealing with linear and affine models showing a fast decay of the Kolmogorov n-width. On one hand, the autoencoder architecture represents a nonlinear generalization of the POD compression procedure, allowing one to encode the main information in a latent set of variables while extracting their main features. On the other hand, Graph Neural Networks (GNNs) constitute a natural framework for studying PDE solutions defined on unstructured meshes. Here, we develop a non-intrusive and data-driven nonlinear reduction approach, exploiting GNNs to encode the reduced manifold and enable fast evaluations of parametrized PDEs. We show the capabilities of the methodology for several models: linear/nonlinear and scalar/vector problems with fast/slow decay in the physically and geometrically parametrized setting. The main properties of our approach consist of (i) high generalizability in the low-data regime even for complex regimes, (ii) physical compliance with general unstructured grids, and (iii) exploitation of pooling and un-pooling operations to learn from scattered data.

Multi-fidelity surrogate modeling using long short-term memory networks

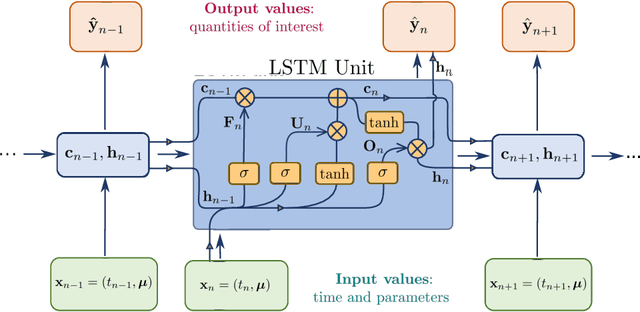
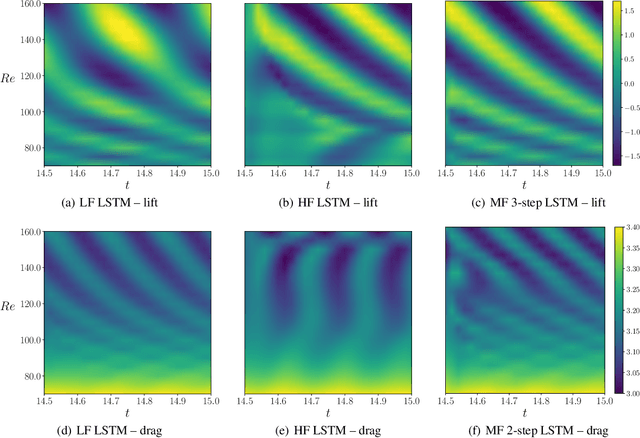
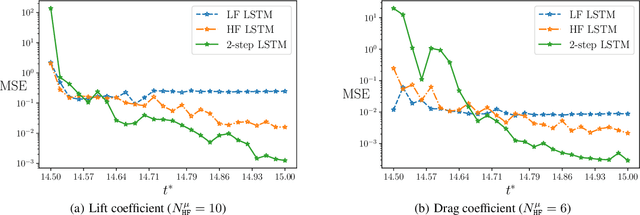
When evaluating quantities of interest that depend on the solutions to differential equations, we inevitably face the trade-off between accuracy and efficiency. Especially for parametrized, time dependent problems in engineering computations, it is often the case that acceptable computational budgets limit the availability of high-fidelity, accurate simulation data. Multi-fidelity surrogate modeling has emerged as an effective strategy to overcome this difficulty. Its key idea is to leverage many low-fidelity simulation data, less accurate but much faster to compute, to improve the approximations with limited high-fidelity data. In this work, we introduce a novel data-driven framework of multi-fidelity surrogate modeling for parametrized, time-dependent problems using long short-term memory (LSTM) networks, to enhance output predictions both for unseen parameter values and forward in time simultaneously - a task known to be particularly challenging for data-driven models. We demonstrate the wide applicability of the proposed approaches in a variety of engineering problems with high- and low-fidelity data generated through fine versus coarse meshes, small versus large time steps, or finite element full-order versus deep learning reduced-order models. Numerical results show that the proposed multi-fidelity LSTM networks not only improve single-fidelity regression significantly, but also outperform the multi-fidelity models based on feed-forward neural networks.

An artificial neural network approach to bifurcating phenomena in computational fluid dynamics

This work deals with the investigation of bifurcating fluid phenomena using a reduced order modelling setting aided by artificial neural networks. We discuss the POD-NN approach dealing with non-smooth solutions set of nonlinear parametrized PDEs. Thus, we study the Navier-Stokes equations describing: (i) the Coanda effect in a channel, and (ii) the lid driven triangular cavity flow, in a physical/geometrical multi-parametrized setting, considering the effects of the domain's configuration on the position of the bifurcation points. Finally, we propose a reduced manifold-based bifurcation diagram for a non-intrusive recovery of the critical points evolution. Exploiting such detection tool, we are able to efficiently obtain information about the pattern flow behaviour, from symmetry breaking profiles to attaching/spreading vortices, even at high Reynolds numbers.

Discovery of slow variables in a class of multiscale stochastic systems via neural networks

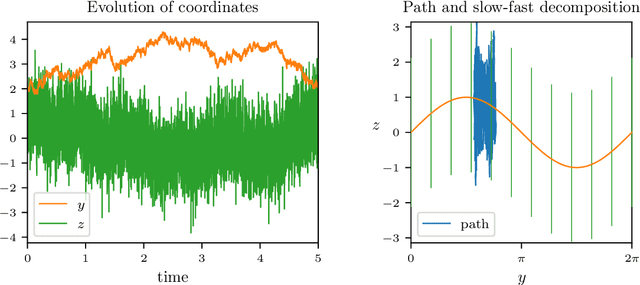
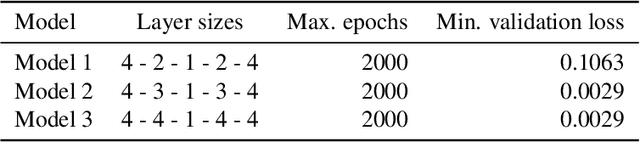
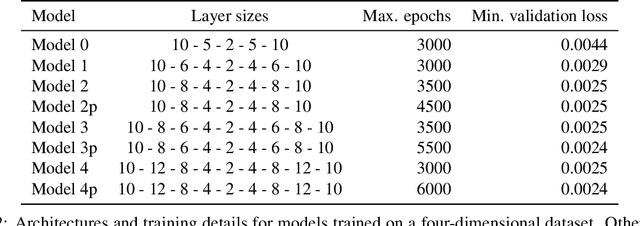
Finding a reduction of complex, high-dimensional dynamics to its essential, low-dimensional "heart" remains a challenging yet necessary prerequisite for designing efficient numerical approaches. Machine learning methods have the potential to provide a general framework to automatically discover such representations. In this paper, we consider multiscale stochastic systems with local slow-fast time scale separation and propose a new method to encode in an artificial neural network a map that extracts the slow representation from the system. The architecture of the network consists of an encoder-decoder pair that we train in a supervised manner to learn the appropriate low-dimensional embedding in the bottleneck layer. We test the method on a number of examples that illustrate the ability to discover a correct slow representation. Moreover, we provide an error measure to assess the quality of the embedding and demonstrate that pruning the network can pinpoint an essential coordinates of the system to build the slow representation.

Efficient numerical room acoustic simulations with parametrized boundaries using the spectral element and reduced basis method

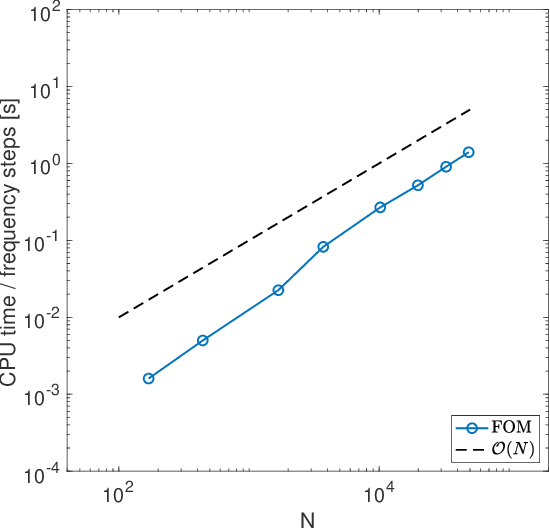
Numerical methods can be used to simulate wave propagation in rooms, with applications in virtual reality and building design. Such methods can be highly accurate but computationally expensive when simulating high frequencies and large domains for long simulation times. Moreover, it is common that solutions are sought for multiple input parameter values, e.g., in design processes in room acoustics, where different boundary absorption properties are evaluated iteratively. We present a framework that combines a spectral element method (SEM) and a reduced basis method (RBM) to achieve a computational cost reduction for parameterized room acoustic simulations. The SEM provides low dispersion and dissipation properties due to the high-order discretization and the RBM reduces the computational burden further when parametrizing the boundary properties for both frequency-independent and dependent conditions. The problem is solved in the Laplace domain, which avoids instability issues on the reduced model. We demonstrate that the use of high-order discretization and model order reduction has significant advantages for room acoustics in terms of computational efficiency and accuracy.

Multi-fidelity regression using artificial neural networks: efficient approximation of parameter-dependent output quantities

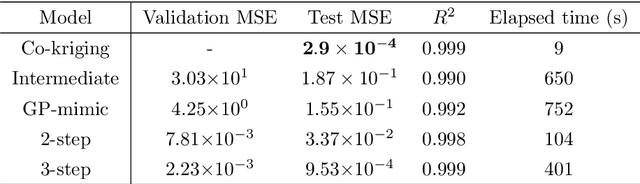
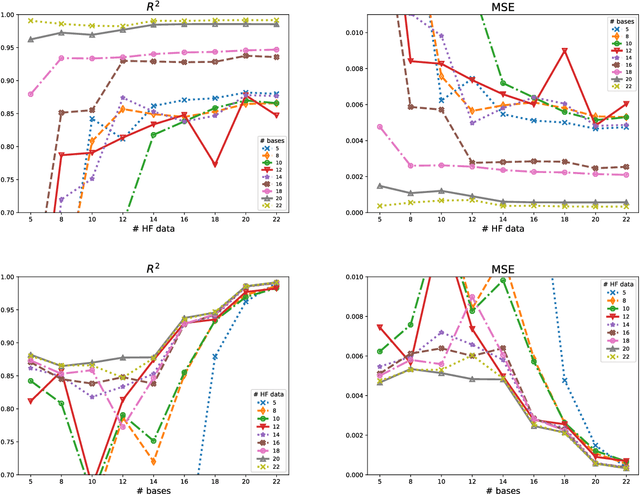
Highly accurate numerical or physical experiments are often time-consuming or expensive to obtain. When time or budget restrictions prohibit the generation of additional data, the amount of available samples may be too limited to provide satisfactory model results. Multi-fidelity methods deal with such problems by incorporating information from other sources, which are ideally well-correlated with the high-fidelity data, but can be obtained at a lower cost. By leveraging correlations between different data sets, multi-fidelity methods often yield superior generalization when compared to models based solely on a small amount of high-fidelity data. In this work, we present the use of artificial neural networks applied to multi-fidelity regression problems. By elaborating a few existing approaches, we propose new neural network architectures for multi-fidelity regression. The introduced models are compared against a traditional multi-fidelity scheme, co-kriging. A collection of artificial benchmarks are presented to measure the performance of the analyzed models. The results show that cross-validation in combination with Bayesian optimization consistently leads to neural network models that outperform the co-kriging scheme. Additionally, we show an application of multi-fidelity regression to an engineering problem. The propagation of a pressure wave into an acoustic horn with parametrized shape and frequency is considered, and the index of reflection intensity is approximated using the multi-fidelity models. A finite element model and a reduced basis model are adopted as the high- and low-fidelity, respectively. It is shown that the multi-fidelity neural network returns outputs that achieve a comparable accuracy to those from the expensive, full-order model, using only very few full-order evaluations combined with a larger amount of inaccurate but cheap evaluations of a reduced order model.

Constraint-Aware Neural Networks for Riemann Problems

Neural networks are increasingly used in complex (data-driven) simulations as surrogates or for accelerating the computation of classical surrogates. In many applications physical constraints, such as mass or energy conservation, must be satisfied to obtain reliable results. However, standard machine learning algorithms are generally not tailored to respect such constraints. We propose two different strategies to generate constraint-aware neural networks. We test their performance in the context of front-capturing schemes for strongly nonlinear wave motion in compressible fluid flow. Precisely, in this context so-called Riemann problems have to be solved as surrogates. Their solution describes the local dynamics of the captured wave front in numerical simulations. Three model problems are considered: a cubic flux model problem, an isothermal two-phase flow model, and the Euler equations. We demonstrate that a decrease in the constraint deviation correlates with low discretization errors for all model problems, in addition to the structural advantage of fulfilling the constraint.