Efficient numerical room acoustic simulations with parametrized boundaries using the spectral element and reduced basis method

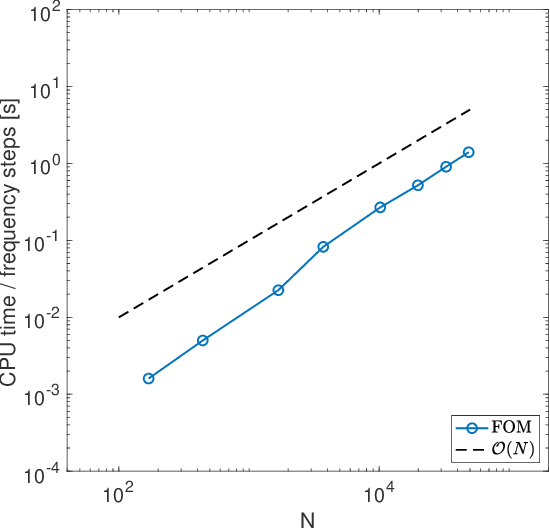
Numerical methods can be used to simulate wave propagation in rooms, with applications in virtual reality and building design. Such methods can be highly accurate but computationally expensive when simulating high frequencies and large domains for long simulation times. Moreover, it is common that solutions are sought for multiple input parameter values, e.g., in design processes in room acoustics, where different boundary absorption properties are evaluated iteratively. We present a framework that combines a spectral element method (SEM) and a reduced basis method (RBM) to achieve a computational cost reduction for parameterized room acoustic simulations. The SEM provides low dispersion and dissipation properties due to the high-order discretization and the RBM reduces the computational burden further when parametrizing the boundary properties for both frequency-independent and dependent conditions. The problem is solved in the Laplace domain, which avoids instability issues on the reduced model. We demonstrate that the use of high-order discretization and model order reduction has significant advantages for room acoustics in terms of computational efficiency and accuracy.