Manifold embedding data-driven mechanics
Paper and Code
Dec 18, 2021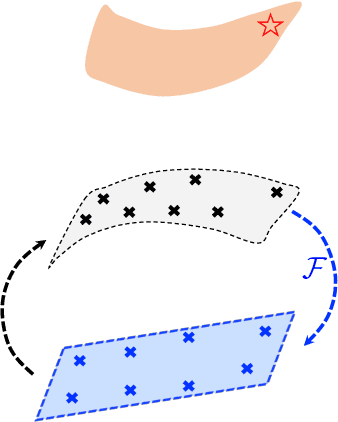
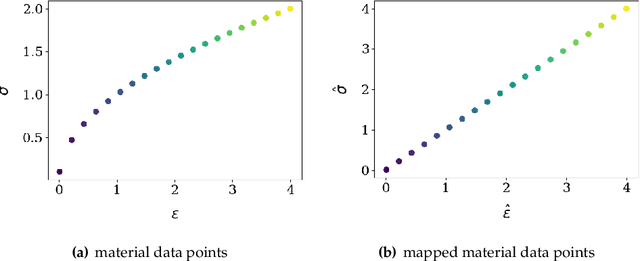
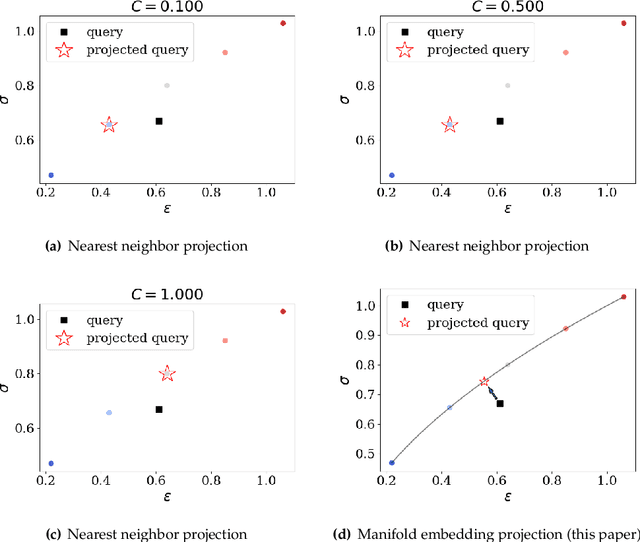
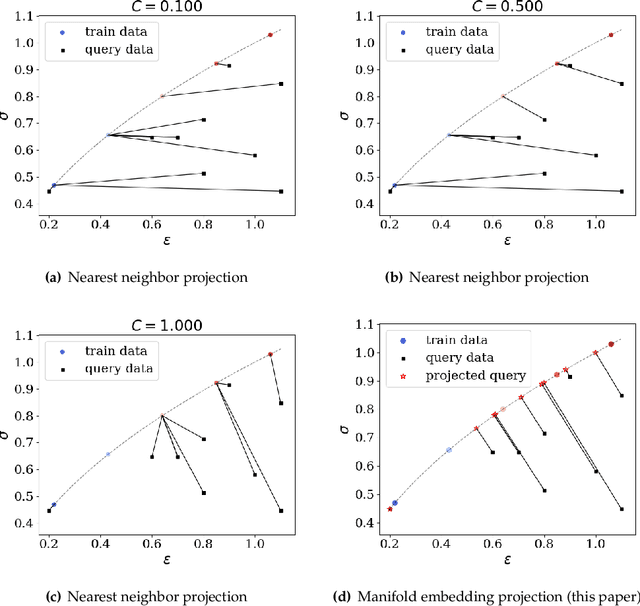
This article introduces a new data-driven approach that leverages a manifold embedding generated by the invertible neural network to improve the robustness, efficiency, and accuracy of the constitutive-law-free simulations with limited data. We achieve this by training a deep neural network to globally map data from the constitutive manifold onto a lower-dimensional Euclidean vector space. As such, we establish the relation between the norm of the mapped Euclidean vector space and the metric of the manifold and lead to a more physically consistent notion of distance for the material data. This treatment in return allows us to bypass the expensive combinatorial optimization, which may significantly speed up the model-free simulations when data are abundant and of high dimensions. Meanwhile, the learning of embedding also improves the robustness of the algorithm when the data is sparse or distributed unevenly in the parametric space. Numerical experiments are provided to demonstrate and measure the performance of the manifold embedding technique under different circumstances. Results obtained from the proposed method and those obtained via the classical energy norms are compared.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge