Embedded-physics machine learning for coarse-graining and collective variable discovery without data

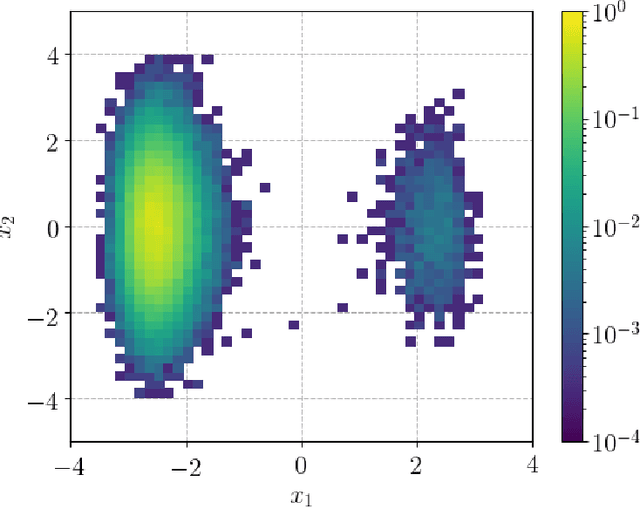
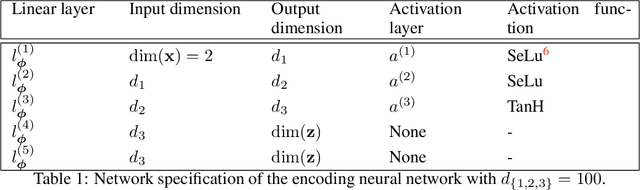
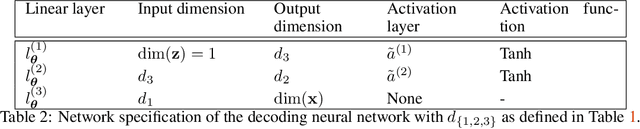
We present a novel learning framework that consistently embeds underlying physics while bypassing a significant drawback of most modern, data-driven coarse-grained approaches in the context of molecular dynamics (MD), i.e., the availability of big data. The generation of a sufficiently large training dataset poses a computationally demanding task, while complete coverage of the atomistic configuration space is not guaranteed. As a result, the explorative capabilities of data-driven coarse-grained models are limited and may yield biased "predictive" tools. We propose a novel objective based on reverse Kullback-Leibler divergence that fully incorporates the available physics in the form of the atomistic force field. Rather than separating model learning from the data-generation procedure - the latter relies on simulating atomistic motions governed by force fields - we query the atomistic force field at sample configurations proposed by the predictive coarse-grained model. Thus, learning relies on the evaluation of the force field but does not require any MD simulation. The resulting generative coarse-grained model serves as an efficient surrogate model for predicting atomistic configurations and estimating relevant observables. Beyond obtaining a predictive coarse-grained model, we demonstrate that in the discovered lower-dimensional representation, the collective variables (CVs) are related to physicochemical properties, which are essential for gaining understanding of unexplored complex systems. We demonstrate the algorithmic advances in terms of predictive ability and the physical meaning of the revealed CVs for a bimodal potential energy function and the alanine dipeptide.

Predictive Collective Variable Discovery with Deep Bayesian Models

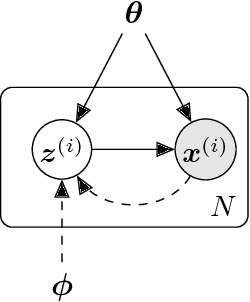
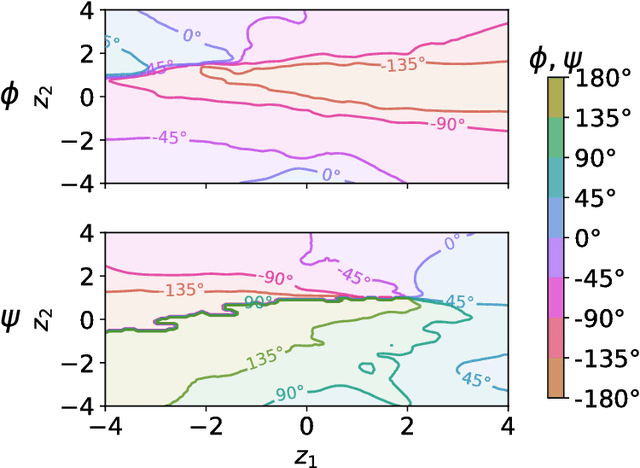
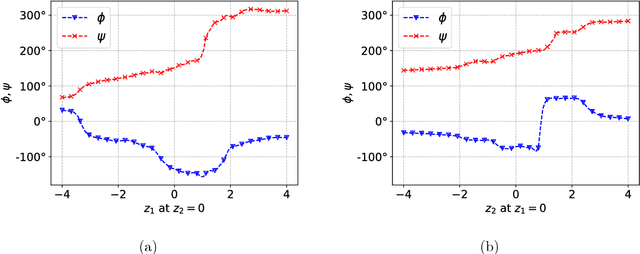
Extending spatio-temporal scale limitations of models for complex atomistic systems considered in biochemistry and materials science necessitates the development of enhanced sampling methods. The potential acceleration in exploring the configurational space by enhanced sampling methods depends on the choice of collective variables (CVs). In this work, we formulate the discovery of CVs as a Bayesian inference problem and consider the CVs as hidden generators of the full-atomistic trajectory. The ability to generate samples of the fine-scale atomistic configurations using limited training data allows us to compute estimates of observables as well as our probabilistic confidence on them. The methodology is based on emerging methodological advances in machine learning and variational inference. The discovered CVs are related to physicochemical properties which are essential for understanding mechanisms especially in unexplored complex systems. We provide a quantitative assessment of the CVs in terms of their predictive ability for alanine dipeptide (ALA-2) and ALA-15 peptide.

Predictive Coarse-Graining

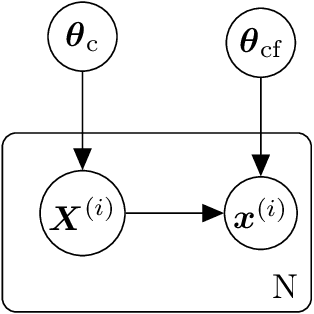
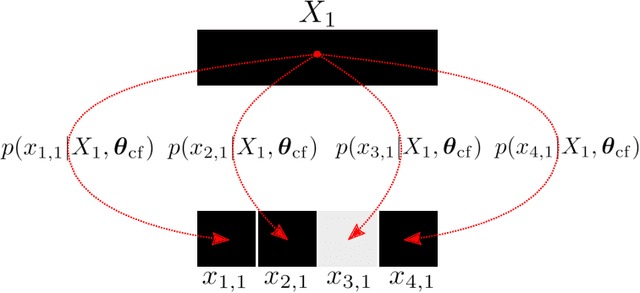
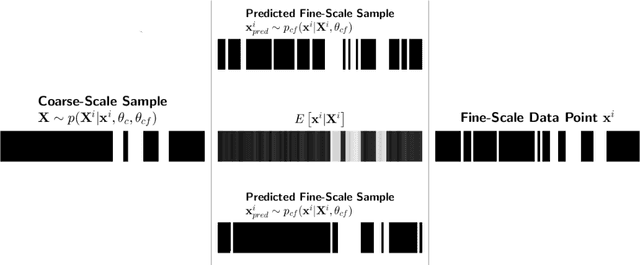
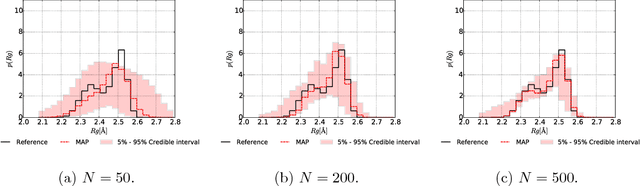
We propose a data-driven, coarse-graining formulation in the context of equilibrium statistical mechanics. In contrast to existing techniques which are based on a fine-to-coarse map, we adopt the opposite strategy by prescribing a probabilistic coarse-to-fine map. This corresponds to a directed probabilistic model where the coarse variables play the role of latent generators of the fine scale (all-atom) data. From an information-theoretic perspective, the framework proposed provides an improvement upon the relative entropy method and is capable of quantifying the uncertainty due to the information loss that unavoidably takes place during the CG process. Furthermore, it can be readily extended to a fully Bayesian model where various sources of uncertainties are reflected in the posterior of the model parameters. The latter can be used to produce not only point estimates of fine-scale reconstructions or macroscopic observables, but more importantly, predictive posterior distributions on these quantities. Predictive posterior distributions reflect the confidence of the model as a function of the amount of data and the level of coarse-graining. The issues of model complexity and model selection are seamlessly addressed by employing a hierarchical prior that favors the discovery of sparse solutions, revealing the most prominent features in the coarse-grained model. A flexible and parallelizable Monte Carlo - Expectation-Maximization (MC-EM) scheme is proposed for carrying out inference and learning tasks. A comparative assessment of the proposed methodology is presented for a lattice spin system and the SPC/E water model.