Transformers for Modeling Physical Systems

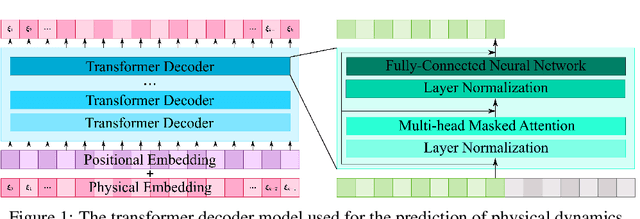
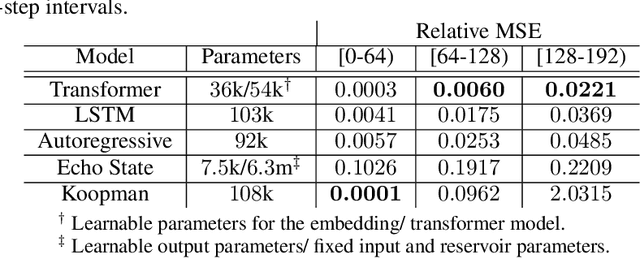
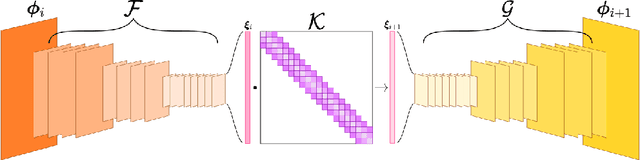
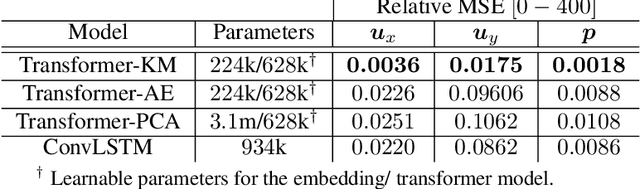
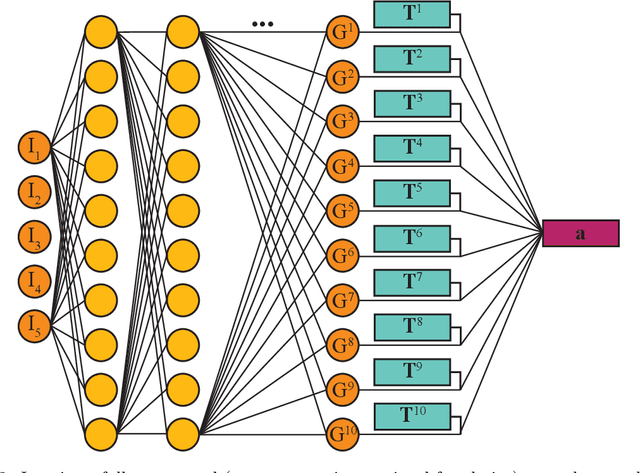
Transformers are widely used in neural language processing due to their ability to model longer-term dependencies in text. Although these models achieve state-of-the-art performance for many language related tasks, their applicability outside of the neural language processing field has been minimal. In this work, we propose the use of transformer models for the prediction of dynamical systems representative of physical phenomena. The use of Koopman based embeddings provide a unique and powerful method for projecting any dynamical system into a vector representation which can then be predicted by a transformer model. The proposed model is able to accurately predict various dynamical systems and outperform classical methods that are commonly used in the scientific machine learning literature.

Multi-fidelity Generative Deep Learning Turbulent Flows

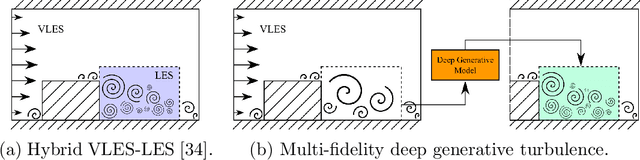
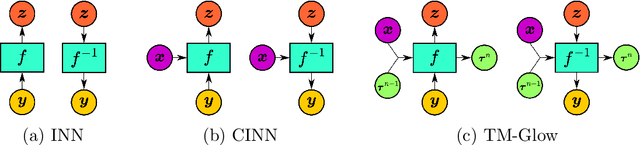
In computational fluid dynamics, there is an inevitable trade off between accuracy and computational cost. Low-fidelity simulations with coarse discretizations are computationally inexpensive, however, the resulting flow fields are often inaccurate. Alternatively, high-fidelity simulations can yield accurate predictions but at exponentially higher computational cost. In this work, a novel multi-fidelity deep generative model is introduced for the surrogate modeling of high-fidelity turbulent flow fields given the solution of a computationally inexpensive but inaccurate low-fidelity solver. The resulting surrogate is able to generate physically accurate turbulent realizations at a computational cost magnitudes lower than that of a high-fidelity simulation. The deep generative model developed is a conditional invertible neural network, built with normalizing flows, with recurrent LSTM connections that allow for stable training of transient systems with high predictive accuracy. The model is trained with a variational loss that combines both data-driven and physics-constrained learning. This deep generative model is applied to non-trivial high Reynolds number flows governed by the Navier-Stokes equations including turbulent flow over a backwards facing step at different Reynolds numbers and turbulent wake behind an array of bluff bodies. For both of these examples, the model is able to generate unique yet physically accurate turbulent fluid flows conditioned on an inexpensive low-fidelity solution.

Modeling the Dynamics of PDE Systems with Physics-Constrained Deep Auto-Regressive Networks

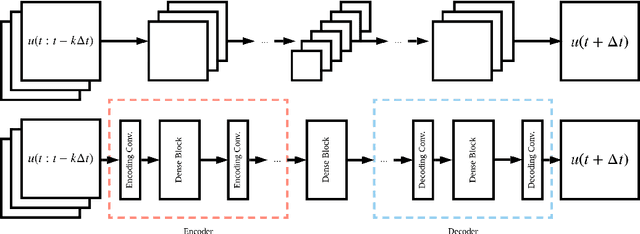
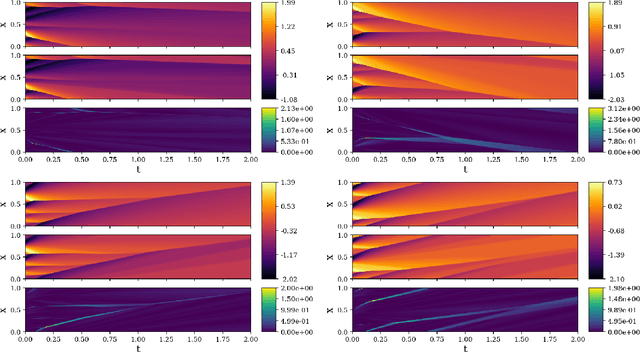
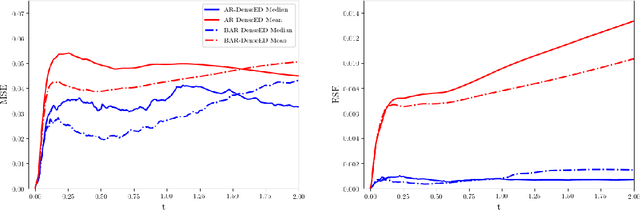
In recent years, deep learning has proven to be a viable methodology for surrogate modeling and uncertainty quantification for a vast number of physical systems. However, in their traditional form, such models require a large amount of training data. This is of particular importance for various engineering and scientific applications where data may be extremely expensive to obtain. To overcome this shortcoming, physics-constrained deep learning provides a promising methodology as it only utilizes the governing equations. In this work, we propose a novel auto-regressive dense encoder-decoder convolutional neural network to solve and model transient systems with non-linear dynamics at a computational cost that is potentially magnitudes lower than standard numerical solvers. This model includes a Bayesian framework that allows for uncertainty quantification of the predicted quantities of interest at each time-step. We rigorously test this model on several non-linear transient partial differential equation systems including the turbulence of the Kuramoto-Sivashinsky equation, multi-shock formation and interaction with 1D Burgers' equation and 2D wave dynamics with coupled Burgers' equations. For each system, the predictive results and uncertainty are presented and discussed together with comparisons to the results obtained from traditional numerical analysis methods.

Quantifying model form uncertainty in Reynolds-averaged turbulence models with Bayesian deep neural networks

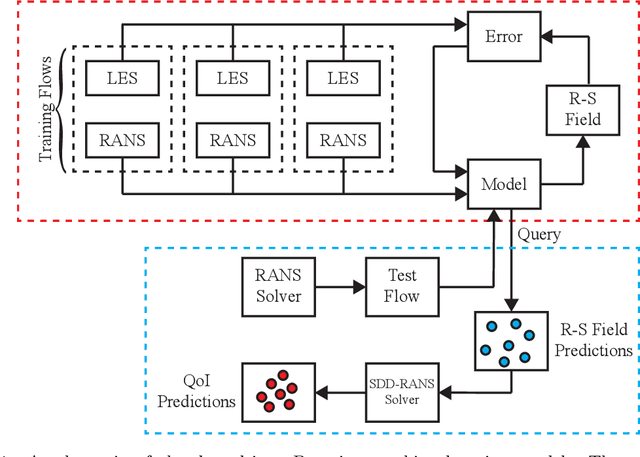
Data-driven methods for improving turbulence modeling in Reynolds-Averaged Navier-Stokes (RANS) simulations have gained significant interest in the computational fluid dynamics community. Modern machine learning models have opened up a new area of black-box turbulence models allowing for the tuning of RANS simulations to increase their predictive accuracy. While several data-driven turbulence models have been reported, the quantification of the uncertainties introduced has mostly been neglected. Uncertainty quantification for such data-driven models is essential since their predictive capability rapidly declines as they are tested for flow physics that deviate from that in the training data. In this work, we propose a novel data-driven framework that not only improves RANS predictions but also provides probabilistic bounds for fluid quantities such as velocity and pressure. The uncertainties capture include both model form uncertainty as well as epistemic uncertainty induced by the limited training data. An invariant Bayesian deep neural network is used to predict the anisotropic tensor component of the Reynolds stress. This model is trained using Stein's variational gradient decent algorithm. The computed uncertainty on the Reynolds stress is propagated to the quantities of interest by vanilla Monte Carlo simulation. Results are presented for two test cases that differ geometrically from the training flows at several different Reynolds numbers. The prediction enhancement of the data-driven model is discussed as well as the associated probabilistic bounds for flow properties of interest. Ultimately this framework allows for a quantitative measurement of model confidence and uncertainty quantification for flows in which no high-fidelity observations or prior knowledge is available.