WENDy for Nonlinear-in-Parameter ODEs

The Weak-form Estimation of Non-linear Dynamics (WENDy) algorithm is extended to accommodate systems of ordinary differential equations that are nonlinear-in-parameters (NiP). The extension rests on derived analytic expressions for a likelihood function, its gradient and its Hessian matrix. WENDy makes use of these to approximate a maximum likelihood estimator based on optimization routines suited for non-convex optimization problems. The resulting parameter estimation algorithm has better accuracy, a substantially larger domain of convergence, and is often orders of magnitude faster than the conventional output error least squares method (based on forward solvers). The WENDy.jl algorithm is efficiently implemented in Julia. We demonstrate the algorithm's ability to accommodate the weak form optimization for both additive normal and multiplicative log-normal noise, and present results on a suite of benchmark systems of ordinary differential equations. In order to demonstrate the practical benefits of our approach, we present extensive comparisons between our method and output error methods in terms of accuracy, precision, bias, and coverage.

Learning Weather Models from Data with WSINDy

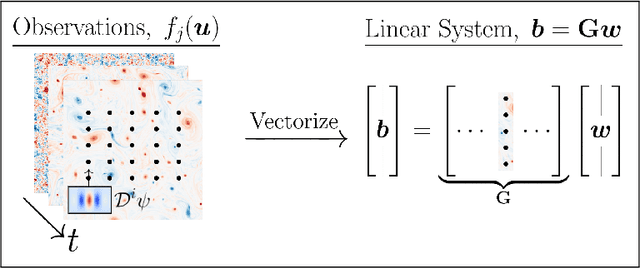
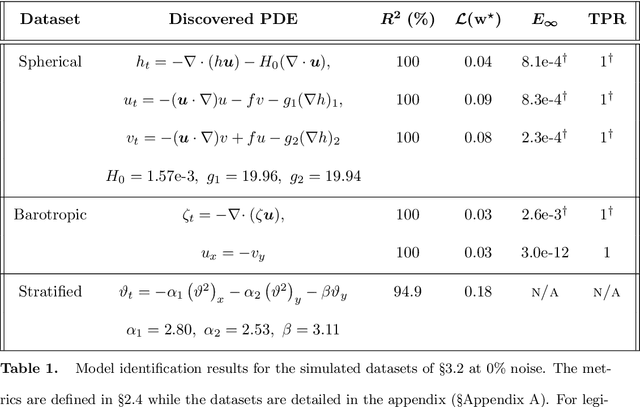
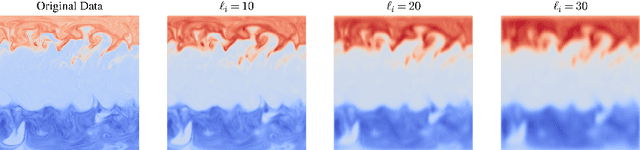
The multiscale and turbulent nature of Earth's atmosphere has historically rendered accurate weather modeling a hard problem. Recently, there has been an explosion of interest surrounding data-driven approaches to weather modeling, which in many cases show improved forecasting accuracy and computational efficiency when compared to traditional methods. However, many of the current data-driven approaches employ highly parameterized neural networks, often resulting in uninterpretable models and limited gains in scientific understanding. In this work, we address the interpretability problem by explicitly discovering partial differential equations governing various weather phenomena, identifying symbolic mathematical models with direct physical interpretations. The purpose of this paper is to demonstrate that, in particular, the Weak form Sparse Identification of Nonlinear Dynamics (WSINDy) algorithm can learn effective weather models from both simulated and assimilated data. Our approach adapts the standard WSINDy algorithm to work with high-dimensional fluid data of arbitrary spatial dimension. Moreover, we develop an approach for handling terms that are not integrable-by-parts, such as advection operators.

The Weak Form Is Stronger Than You Think

The weak form is a ubiquitous, well-studied, and widely-utilized mathematical tool in modern computational and applied mathematics. In this work we provide a survey of both the history and recent developments for several fields in which the weak form can play a critical role. In particular, we highlight several recent advances in weak form versions of equation learning, parameter estimation, and coarse graining, which offer surprising noise robustness, accuracy, and computational efficiency. We note that this manuscript is a companion piece to our October 2024 SIAM News article of the same name. Here we provide more detailed explanations of mathematical developments as well as a more complete list of references. Lastly, we note that the software with which to reproduce the results in this manuscript is also available on our group's GitHub website https://github.com/MathBioCU .

A Comprehensive Review of Latent Space Dynamics Identification Algorithms for Intrusive and Non-Intrusive Reduced-Order-Modeling

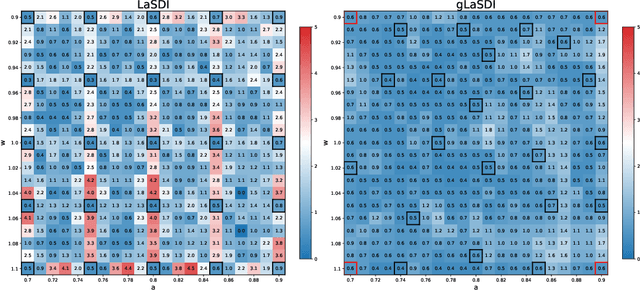
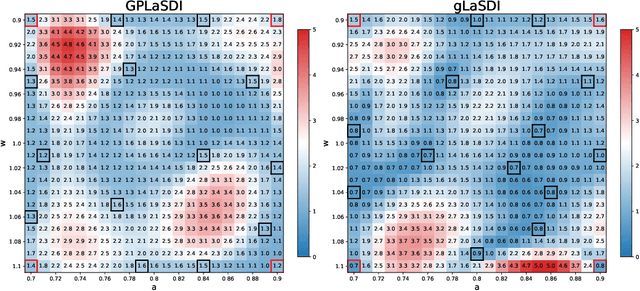
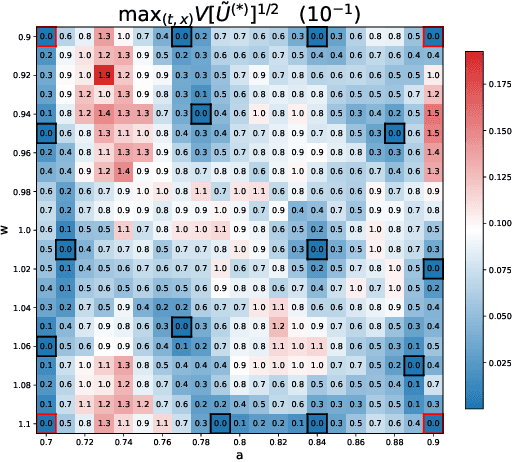
Numerical solvers of partial differential equations (PDEs) have been widely employed for simulating physical systems. However, the computational cost remains a major bottleneck in various scientific and engineering applications, which has motivated the development of reduced-order models (ROMs). Recently, machine-learning-based ROMs have gained significant popularity and are promising for addressing some limitations of traditional ROM methods, especially for advection dominated systems. In this chapter, we focus on a particular framework known as Latent Space Dynamics Identification (LaSDI), which transforms the high-fidelity data, governed by a PDE, to simpler and low-dimensional latent-space data, governed by ordinary differential equations (ODEs). These ODEs can be learned and subsequently interpolated to make ROM predictions. Each building block of LaSDI can be easily modulated depending on the application, which makes the LaSDI framework highly flexible. In particular, we present strategies to enforce the laws of thermodynamics into LaSDI models (tLaSDI), enhance robustness in the presence of noise through the weak form (WLaSDI), select high-fidelity training data efficiently through active learning (gLaSDI, GPLaSDI), and quantify the ROM prediction uncertainty through Gaussian processes (GPLaSDI). We demonstrate the performance of different LaSDI approaches on Burgers equation, a non-linear heat conduction problem, and a plasma physics problem, showing that LaSDI algorithms can achieve relative errors of less than a few percent and up to thousands of times speed-ups.

Weak-Form Latent Space Dynamics Identification

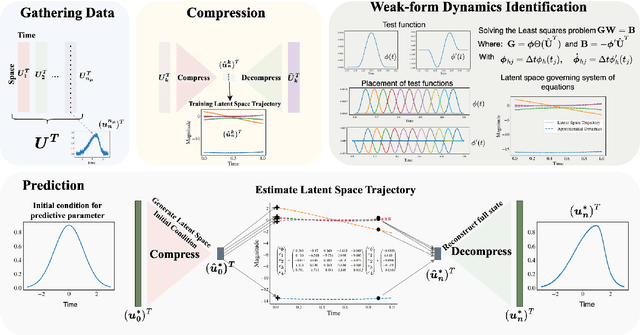
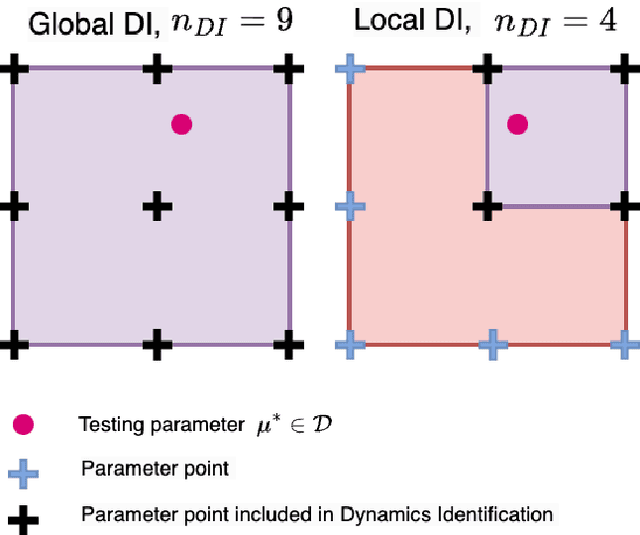
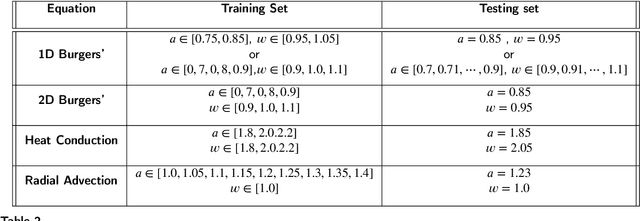
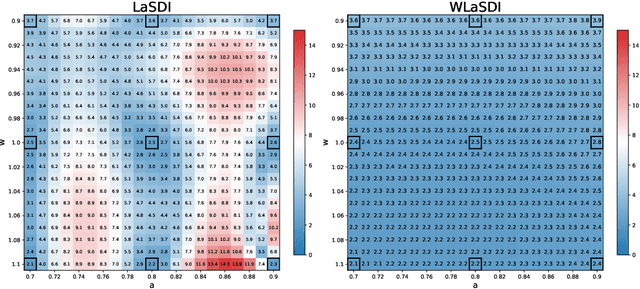
Recent work in data-driven modeling has demonstrated that a weak formulation of model equations enhances the noise robustness of a wide range of computational methods. In this paper, we demonstrate the power of the weak form to enhance the LaSDI (Latent Space Dynamics Identification) algorithm, a recently developed data-driven reduced order modeling technique. We introduce a weak form-based version WLaSDI (Weak-form Latent Space Dynamics Identification). WLaSDI first compresses data, then projects onto the test functions and learns the local latent space models. Notably, WLaSDI demonstrates significantly enhanced robustness to noise. With WLaSDI, the local latent space is obtained using weak-form equation learning techniques. Compared to the standard sparse identification of nonlinear dynamics (SINDy) used in LaSDI, the variance reduction of the weak form guarantees a robust and precise latent space recovery, hence allowing for a fast, robust, and accurate simulation. We demonstrate the efficacy of WLaSDI vs. LaSDI on several common benchmark examples including viscid and inviscid Burgers', radial advection, and heat conduction. For instance, in the case of 1D inviscid Burgers' simulations with the addition of up to 100% Gaussian white noise, the relative error remains consistently below 6% for WLaSDI, while it can exceed 10,000% for LaSDI. Similarly, for radial advection simulations, the relative errors stay below 15% for WLaSDI, in stark contrast to the potential errors of up to 10,000% with LaSDI. Moreover, speedups of several orders of magnitude can be obtained with WLaSDI. For example applying WLaSDI to 1D Burgers' yields a 140X speedup compared to the corresponding full order model. Python code to reproduce the results in this work is available at (https://github.com/MathBioCU/PyWSINDy_ODE) and (https://github.com/MathBioCU/PyWLaSDI).

Coarse-Graining Hamiltonian Systems Using WSINDy

The Weak-form Sparse Identification of Nonlinear Dynamics algorithm (WSINDy) has been demonstrated to offer coarse-graining capabilities in the context of interacting particle systems ( https://doi.org/10.1016/j.physd.2022.133406 ). In this work we extend this capability to the problem of coarse-graining Hamiltonian dynamics which possess approximate symmetries. Such approximate symmetries often lead to the existence of a Hamiltonian system of reduced dimension that may be used to efficiently capture the dynamics of the relevant degrees of freedom. Deriving such reduced systems, or approximating them numerically, is an ongoing challenge. We demonstrate that WSINDy can successfully identify this reduced Hamiltonian system in the presence of large perturbations imparted from both the inexact nature of the symmetry and extrinsic noise. This is significant in part due to the nontrivial means by which such systems are derived analytically. WSINDy naturally preserves the Hamiltonian structure by restricting to a trial basis of Hamiltonian vector fields, and the methodology is computational efficient, often requiring only a single trajectory to learn the full reduced Hamiltonian, and avoiding forward solves in the learning process. In this way, we argue that weak-form equation learning is particularly well-suited for Hamiltonian coarse-graining. Using nearly-periodic Hamiltonian systems as a prototypical class of systems with approximate symmetries, we show that WSINDy robustly identifies the correct leading-order reduced system of dimension $2(N-1)$ or $N$ from the original $(2N)$-dimensional system, upon observation of the relevant degrees of freedom. We provide physically relevant examples, namely coupled oscillator dynamics, the H\'enon-Heiles system for stellar motion within a galaxy, and the dynamics of charged particles.

Direct Estimation of Parameters in ODE Models Using WENDy: Weak-form Estimation of Nonlinear Dynamics

We introduce the Weak-form Estimation of Nonlinear Dynamics (WENDy) method for estimating model parameters for non-linear systems of ODEs. The core mathematical idea involves an efficient conversion of the strong form representation of a model to its weak form, and then solving a regression problem to perform parameter inference. The core statistical idea rests on the Errors-In-Variables framework, which necessitates the use of the iteratively reweighted least squares algorithm. Further improvements are obtained by using orthonormal test functions, created from a set of $C^{\infty}$ bump functions of varying support sizes. We demonstrate that WENDy is a highly robust and efficient method for parameter inference in differential equations. Without relying on any numerical differential equation solvers, WENDy computes accurate estimates and is robust to large (biologically relevant) levels of measurement noise. For low dimensional systems with modest amounts of data, WENDy is competitive with conventional forward solver-based nonlinear least squares methods in terms of speed and accuracy. For both higher dimensional systems and stiff systems, WENDy is typically both faster (often by orders of magnitude) and more accurate than forward solver-based approaches. We illustrate the method and its performance in some common population and neuroscience models, including logistic growth, Lotka-Volterra, FitzHugh-Nagumo, Hindmarsh-Rose, and a Protein Transduction Benchmark model. Software and code for reproducing the examples is available at (https://github.com/MathBioCU/WENDy).

Asymptotic consistency of the WSINDy algorithm in the limit of continuum data

In this work we study the asymptotic consistency of the weak-form sparse identification of nonlinear dynamics algorithm (WSINDy) in the identification of differential equations from noisy samples of solutions. We prove that the WSINDy estimator is unconditionally asymptotically consistent for a wide class of models which includes the Navier-Stokes equations and the Kuramoto-Sivashinsky equation. We thus provide a mathematically rigorous explanation for the observed robustness to noise of weak-form equation learning. Conversely, we also show that in general the WSINDy estimator is only conditionally asymptotically consistent, yielding discovery of spurious terms with probability one if the noise level is above some critical threshold and the nonlinearities exhibit sufficiently fast growth. We derive explicit bounds on the critical noise threshold in the case of Gaussian white noise and provide an explicit characterization of these spurious terms in the case of trigonometric and/or polynomial model nonlinearities. However, a silver lining to this negative result is that if the data is suitably denoised (a simple moving average filter is sufficient), then we recover unconditional asymptotic consistency on the class of models with locally-Lipschitz nonlinearities. Altogether, our results reveal several important aspects of weak-form equation learning which may be used to improve future algorithms. We demonstrate our results numerically using the Lorenz system, the cubic oscillator, a viscous Burgers growth model, and a Kuramoto-Sivashinsky-type higher-order PDE.

Learning Anisotropic Interaction Rules from Individual Trajectories in a Heterogeneous Cellular Population

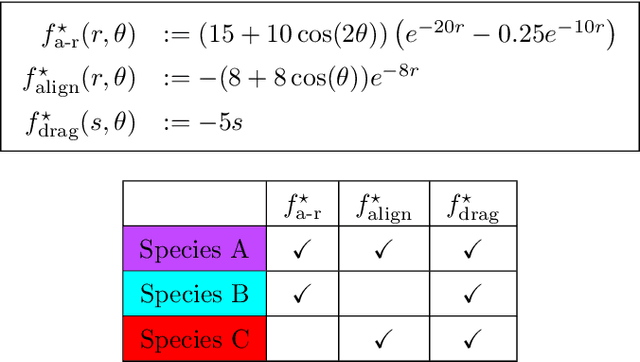
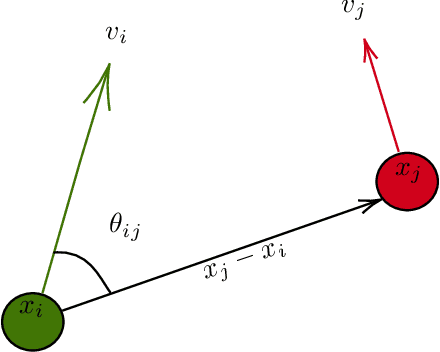
Interacting particle system (IPS) models have proven to be highly successful for describing the spatial movement of organisms. However, it has proven challenging to infer the interaction rules directly from data. In the field of equation discovery, the Weak form Sparse Identification of Nonlinear Dynamics (WSINDy) methodology has been shown to be very computationally efficient for identifying the governing equations of complex systems, even in the presence of substantial noise. Motivated by the success of IPS models to describe the spatial movement of organisms, we develop WSINDy for second order IPSs to model the movement of communities of cells. Specifically, our approach learns the directional interaction rules that govern the dynamics of a heterogeneous population of migrating cells. Rather than aggregating cellular trajectory data into a single best-fit model, we learn the models for each individual cell. These models can then be efficiently classified according to the active classes of interactions present in the model. From these classifications, aggregated models are constructed hierarchically to simultaneously identify different species of cells present in the population and determine best-fit models for each species. We demonstrate the efficiency and proficiency of the method on several test scenarios, motivated by common cell migration experiments.

Online Weak-form Sparse Identification of Partial Differential Equations

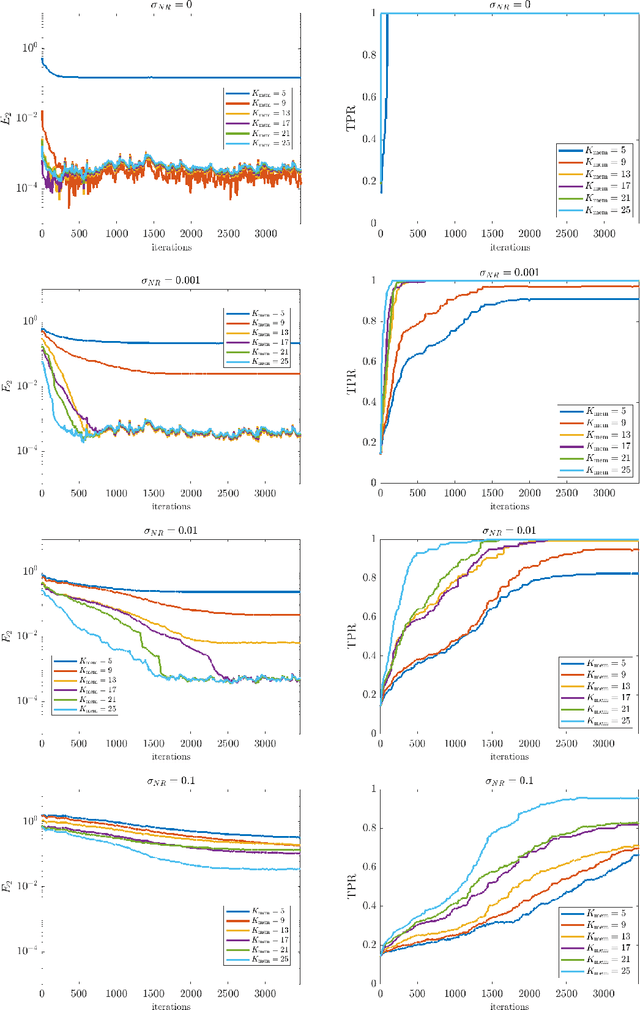
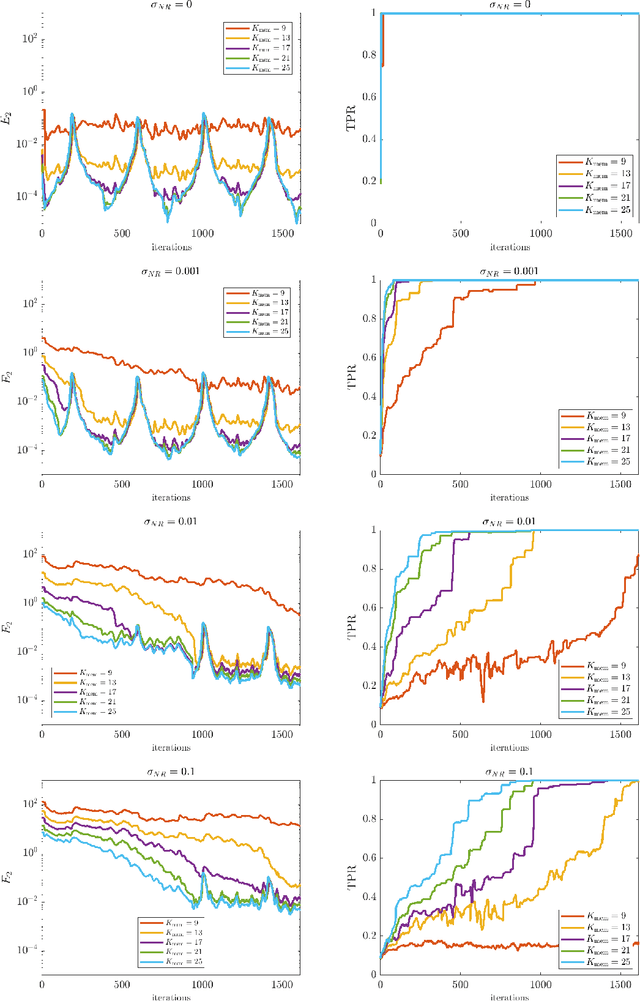
This paper presents an online algorithm for identification of partial differential equations (PDEs) based on the weak-form sparse identification of nonlinear dynamics algorithm (WSINDy). The algorithm is online in a sense that if performs the identification task by processing solution snapshots that arrive sequentially. The core of the method combines a weak-form discretization of candidate PDEs with an online proximal gradient descent approach to the sparse regression problem. In particular, we do not regularize the $\ell_0$-pseudo-norm, instead finding that directly applying its proximal operator (which corresponds to a hard thresholding) leads to efficient online system identification from noisy data. We demonstrate the success of the method on the Kuramoto-Sivashinsky equation, the nonlinear wave equation with time-varying wavespeed, and the linear wave equation, in one, two, and three spatial dimensions, respectively. In particular, our examples show that the method is capable of identifying and tracking systems with coefficients that vary abruptly in time, and offers a streaming alternative to problems in higher dimensions.