On the Sample Complexity of Learning with Geometric Stability

Many supervised learning problems involve high-dimensional data such as images, text, or graphs. In order to make efficient use of data, it is often useful to leverage certain geometric priors in the problem at hand, such as invariance to translations, permutation subgroups, or stability to small deformations. We study the sample complexity of learning problems where the target function presents such invariance and stability properties, by considering spherical harmonic decompositions of such functions on the sphere. We provide non-parametric rates of convergence for kernel methods, and show improvements in sample complexity by a factor equal to the size of the group when using an invariant kernel over the group, compared to the corresponding non-invariant kernel. These improvements are valid when the sample size is large enough, with an asymptotic behavior that depends on spectral properties of the group. Finally, these gains are extended beyond invariance groups to also cover geometric stability to small deformations, modeled here as subsets (not necessarily subgroups) of permutations.

Multilevel Stein variational gradient descent with applications to Bayesian inverse problems

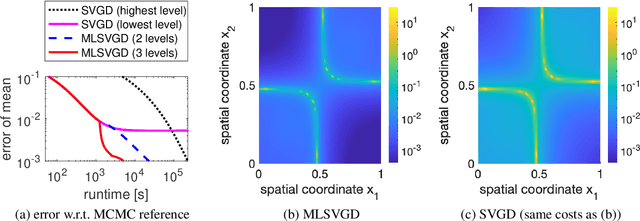
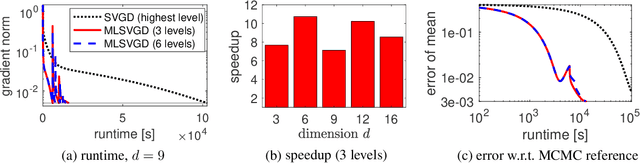
This work presents a multilevel variant of Stein variational gradient descent to more efficiently sample from target distributions. The key ingredient is a sequence of distributions with growing fidelity and costs that converges to the target distribution of interest. For example, such a sequence of distributions is given by a hierarchy of ever finer discretization levels of the forward model in Bayesian inverse problems. The proposed multilevel Stein variational gradient descent moves most of the iterations to lower, cheaper levels with the aim of requiring only a few iterations on the higher, more expensive levels when compared to the traditional, single-level Stein variational gradient descent variant that uses the highest-level distribution only. Under certain assumptions, in the mean-field limit, the error of the proposed multilevel Stein method decays by a log factor faster than the error of the single-level counterpart with respect to computational costs. Numerical experiments with Bayesian inverse problems show speedups of more than one order of magnitude of the proposed multilevel Stein method compared to the single-level variant that uses the highest level only.

Depth separation beyond radial functions

High-dimensional depth separation results for neural networks show that certain functions can be efficiently approximated by two-hidden-layer networks but not by one-hidden-layer ones in high-dimensions $d$. Existing results of this type mainly focus on functions with an underlying radial or one-dimensional structure, which are usually not encountered in practice. The first contribution of this paper is to extend such results to a more general class of functions, namely functions with piece-wise oscillatory structure, by building on the proof strategy of (Eldan and Shamir, 2016). We complement these results by showing that, if the domain radius and the rate of oscillation of the objective function are constant, then approximation by one-hidden-layer networks holds at a $\mathrm{poly}(d)$ rate for any fixed error threshold. A common theme in the proof of such results is the fact that one-hidden-layer networks fail to approximate high-energy functions whose Fourier representation is spread in the domain. On the other hand, existing approximation results of a function by one-hidden-layer neural networks rely on the function having a sparse Fourier representation. The choice of the domain also represents a source of gaps between upper and lower approximation bounds. Focusing on a fixed approximation domain, namely the sphere $\mathbb{S}^{d-1}$ in dimension $d$, we provide a characterization of both functions which are efficiently approximable by one-hidden-layer networks and of functions which are provably not, in terms of their Fourier expansion.

Depth separation for reduced deep networks in nonlinear model reduction: Distilling shock waves in nonlinear hyperbolic problems

Classical reduced models are low-rank approximations using a fixed basis designed to achieve dimensionality reduction of large-scale systems. In this work, we introduce reduced deep networks, a generalization of classical reduced models formulated as deep neural networks. We prove depth separation results showing that reduced deep networks approximate solutions of parametrized hyperbolic partial differential equations with approximation error $\epsilon$ with $\mathcal{O}(|\log(\epsilon)|)$ degrees of freedom, even in the nonlinear setting where solutions exhibit shock waves. We also show that classical reduced models achieve exponentially worse approximation rates by establishing lower bounds on the relevant Kolmogorov $N$-widths.

Diffusion-based Deep Active Learning

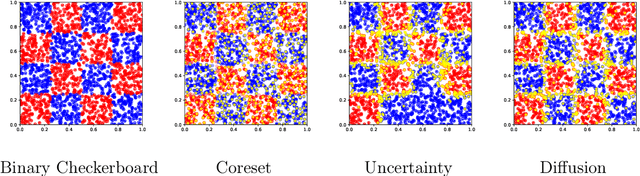
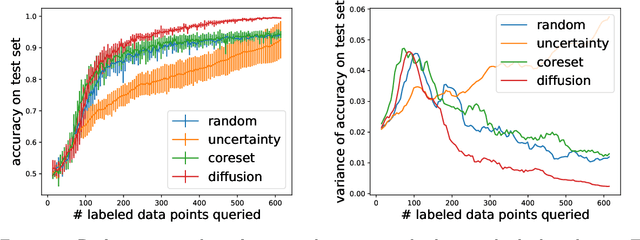
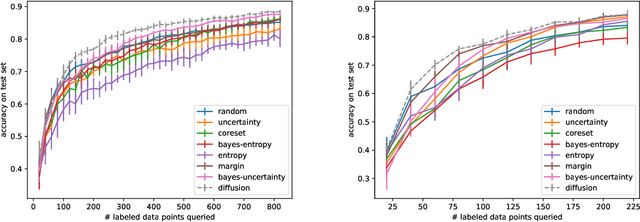
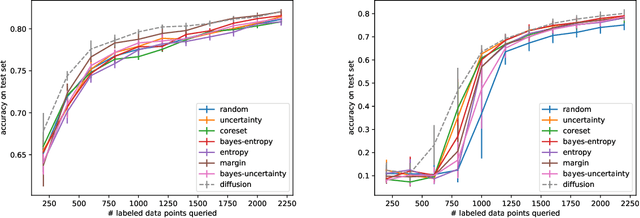
The remarkable performance of deep neural networks depends on the availability of massive labeled data. To alleviate the load of data annotation, active deep learning aims to select a minimal set of training points to be labelled which yields maximal model accuracy. Most existing approaches implement either an `exploration'-type selection criterion, which aims at exploring the joint distribution of data and labels, or a `refinement'-type criterion which aims at localizing the detected decision boundaries. We propose a versatile and efficient criterion that automatically switches from exploration to refinement when the distribution has been sufficiently mapped. Our criterion relies on a process of diffusing the existing label information over a graph constructed from the hidden representation of the data set as provided by the neural network. This graph representation captures the intrinsic geometry of the approximated labeling function. The diffusion-based criterion is shown to be advantageous as it outperforms existing criteria for deep active learning.

Spurious Valleys in Two-layer Neural Network Optimization Landscapes

Neural networks provide a rich class of high-dimensional, non-convex optimization problems. Despite their non-convexity, gradient-descent methods often successfully optimize these models. This has motivated a recent spur in research attempting to characterize properties of their loss surface that may explain such success. In this paper, we address this phenomenon by studying a key topological property of the loss: the presence or absence of spurious valleys, defined as connected components of sub-level sets that do not include a global minimum. Focusing on a class of two-layer neural networks defined by smooth (but generally non-linear) activation functions, we identify a notion of intrinsic dimension and show that it provides necessary and sufficient conditions for the absence of spurious valleys. More concretely, finite intrinsic dimension guarantees that for sufficiently overparametrised models no spurious valleys exist, independently of the data distribution. Conversely, infinite intrinsic dimension implies that spurious valleys do exist for certain data distributions, independently of model overparametrisation. Besides these positive and negative results, we show that, although spurious valleys may exist in general, they are confined to low risk levels and avoided with high probability on overparametrised models.

Learning the Kernel for Classification and Regression

We investigate a series of learning kernel problems with polynomial combinations of base kernels, which will help us solve regression and classification problems. We also perform some numerical experiments of polynomial kernels with regression and classification tasks on different datasets.