Latent Space Energy-based Neural ODEs
Paper and Code
Sep 05, 2024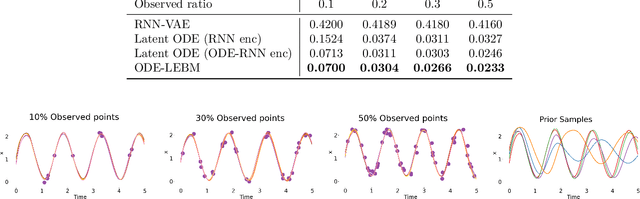


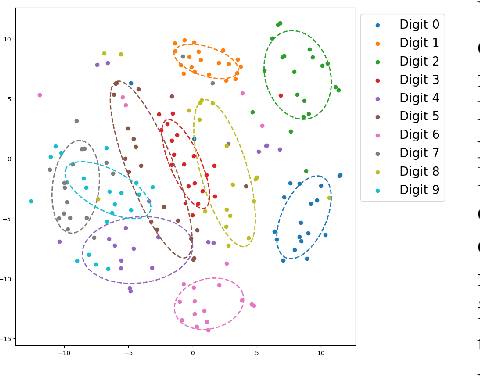
This paper introduces a novel family of deep dynamical models designed to represent continuous-time sequence data. This family of models generates each data point in the time series by a neural emission model, which is a non-linear transformation of a latent state vector. The trajectory of the latent states is implicitly described by a neural ordinary differential equation (ODE), with the initial state following an informative prior distribution parameterized by an energy-based model. Furthermore, we can extend this model to disentangle dynamic states from underlying static factors of variation, represented as time-invariant variables in the latent space. We train the model using maximum likelihood estimation with Markov chain Monte Carlo (MCMC) in an end-to-end manner, without requiring additional assisting components such as an inference network. Our experiments on oscillating systems, videos and real-world state sequences (MuJoCo) illustrate that ODEs with the learnable energy-based prior outperform existing counterparts, and can generalize to new dynamic parameterization, enabling long-horizon predictions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge