Automatic selection of the best neural architecture for time series forecasting via multi-objective optimization and Pareto optimality conditions

Time series forecasting plays a pivotal role in a wide range of applications, including weather prediction, healthcare, structural health monitoring, predictive maintenance, energy systems, and financial markets. While models such as LSTM, GRU, Transformers, and State-Space Models (SSMs) have become standard tools in this domain, selecting the optimal architecture remains a challenge. Performance comparisons often depend on evaluation metrics and the datasets under analysis, making the choice of a universally optimal model controversial. In this work, we introduce a flexible automated framework for time series forecasting that systematically designs and evaluates diverse network architectures by integrating LSTM, GRU, multi-head Attention, and SSM blocks. Using a multi-objective optimization approach, our framework determines the number, sequence, and combination of blocks to align with specific requirements and evaluation objectives. From the resulting Pareto-optimal architectures, the best model for a given context is selected via a user-defined preference function. We validate our framework across four distinct real-world applications. Results show that a single-layer GRU or LSTM is usually optimal when minimizing training time alone. However, when maximizing accuracy or balancing multiple objectives, the best architectures are often composite designs incorporating multiple block types in specific configurations. By employing a weighted preference function, users can resolve trade-offs between objectives, revealing novel, context-specific optimal architectures. Our findings underscore that no single neural architecture is universally optimal for time series forecasting. Instead, the best-performing model emerges as a data-driven composite architecture tailored to user-defined criteria and evaluation objectives.

On the Convergence and generalization of Physics Informed Neural Networks

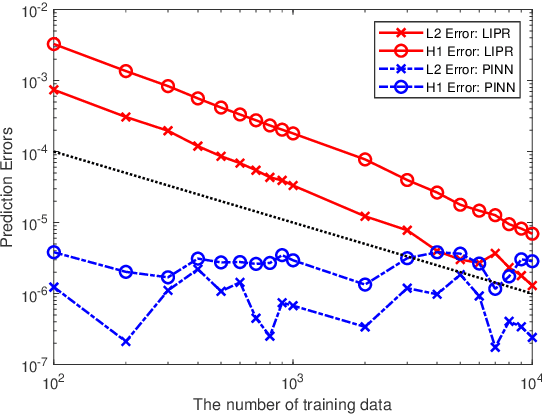
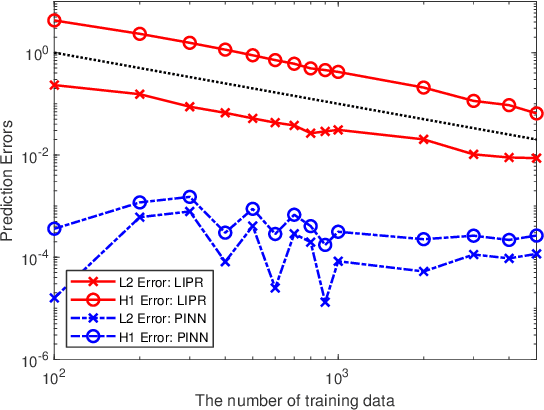
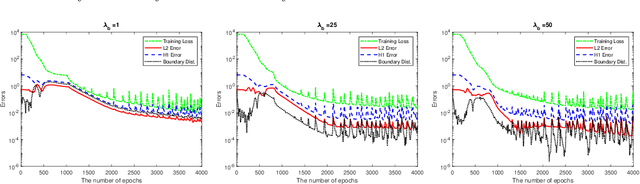
Physics informed neural networks (PINNs) are deep learning based techniques for solving partial differential equations (PDEs). Guided by data and physical laws, PINNs find a neural network that approximates the solution to a system of PDEs. Such a neural network is obtained by minimizing a loss function in which any prior knowledge of PDEs and data are encoded. Despite its remarkable empirical success, there is little theoretical justification for PINNs. In this paper, we establish a mathematical foundation of the PINNs methodology. As the number of data grows, PINNs generate a sequence of minimizers which correspond to a sequence of neural networks. We want to answer the question: Does the sequence of minimizers converge to the solution to the PDE? This question is also related to the generalization of PINNs. We consider two classes of PDEs: elliptic and parabolic. By adapting the Schuader approach, we show that the sequence of minimizers strongly converges to the PDE solution in $L^2$. Furthermore, we show that if each minimizer satisfies the initial/boundary conditions, the convergence mode can be improved to $H^1$. Computational examples are provided to illustrate our theoretical findings. To the best of our knowledge, this is the first theoretical work that shows the consistency of the PINNs methodology.