Data-Driven, Parameterized Reduced-order Models for Predicting Distortion in Metal 3D Printing

In Laser Powder Bed Fusion (LPBF), the applied laser energy produces high thermal gradients that lead to unacceptable final part distortion. Accurate distortion prediction is essential for optimizing the 3D printing process and manufacturing a part that meets geometric accuracy requirements. This study introduces data-driven parameterized reduced-order models (ROMs) to predict distortion in LPBF across various machine process settings. We propose a ROM framework that combines Proper Orthogonal Decomposition (POD) with Gaussian Process Regression (GPR) and compare its performance against a deep-learning based parameterized graph convolutional autoencoder (GCA). The POD-GPR model demonstrates high accuracy, predicting distortions within $\pm0.001mm$, and delivers a computational speed-up of approximately 1800x.

Harnessing Loss Decomposition for Long-Horizon Wave Predictions via Deep Neural Networks

Accurate prediction over long time horizons is crucial for modeling complex physical processes such as wave propagation. Although deep neural networks show promise for real-time forecasting, they often struggle with accumulating phase and amplitude errors as predictions extend over a long period. To address this issue, we propose a novel loss decomposition strategy that breaks down the loss into separate phase and amplitude components. This technique improves the long-term prediction accuracy of neural networks in wave propagation tasks by explicitly accounting for numerical errors, improving stability, and reducing error accumulation over extended forecasts.

Continual Learning of Range-Dependent Transmission Loss for Underwater Acoustic using Conditional Convolutional Neural Net

There is a significant need for precise and reliable forecasting of the far-field noise emanating from shipping vessels. Conventional full-order models based on the Navier-Stokes equations are unsuitable, and sophisticated model reduction methods may be ineffective for accurately predicting far-field noise in environments with seamounts and significant variations in bathymetry. Recent advances in reduced-order models, particularly those based on convolutional and recurrent neural networks, offer a faster and more accurate alternative. These models use convolutional neural networks to reduce data dimensions effectively. However, current deep-learning models face challenges in predicting wave propagation over long periods and for remote locations, often relying on auto-regressive prediction and lacking far-field bathymetry information. This research aims to improve the accuracy of deep-learning models for predicting underwater radiated noise in far-field scenarios. We propose a novel range-conditional convolutional neural network that incorporates ocean bathymetry data into the input. By integrating this architecture into a continual learning framework, we aim to generalize the model for varying bathymetry worldwide. To demonstrate the effectiveness of our approach, we analyze our model on several test cases and a benchmark scenario involving far-field prediction over Dickin's seamount in the Northeast Pacific. Our proposed architecture effectively captures transmission loss over a range-dependent, varying bathymetry profile. This architecture can be integrated into an adaptive management system for underwater radiated noise, providing real-time end-to-end mapping between near-field ship noise sources and received noise at the marine mammal's location.

Node-Element Hypergraph Message Passing for Fluid Dynamics Simulations

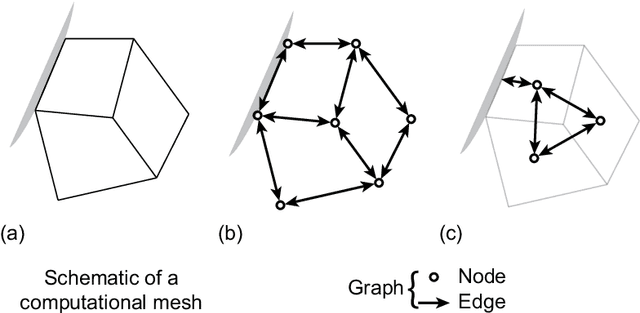
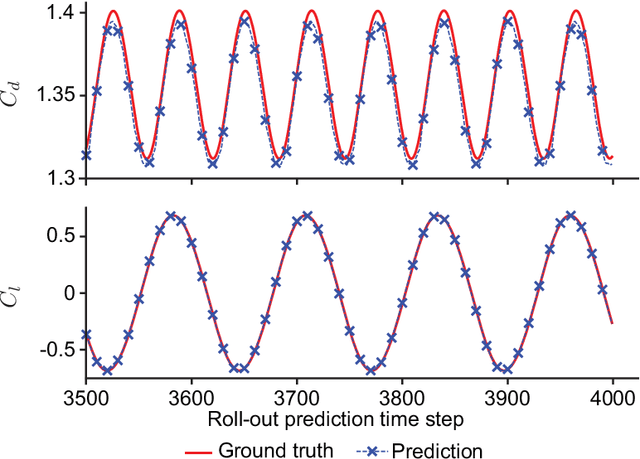
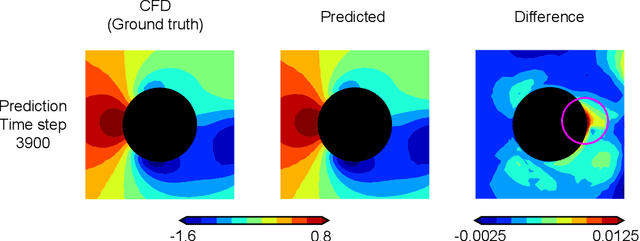
A recent trend in deep learning research features the application of graph neural networks for mesh-based continuum mechanics simulations. Most of these frameworks operate on graphs in which each edge connects two nodes. Inspired by the data connectivity in the finite element method, we connect the nodes by elements rather than edges, effectively forming a hypergraph. We implement a message-passing network on such a node-element hypergraph and explore the capability of the network for the modeling of fluid flow. The network is tested on two common benchmark problems, namely the fluid flow around a circular cylinder and airfoil configurations. The results show that such a message-passing network defined on the node-element hypergraph is able to generate more stable and accurate temporal roll-out predictions compared to the baseline generalized message-passing network defined on a normal graph. Along with adjustments in activation function and training loss, we expect this work to set a new strong baseline for future explorations of mesh-based fluid simulations with graph neural networks.

Combined space-time reduced-order model with 3D deep convolution for extrapolating fluid dynamics

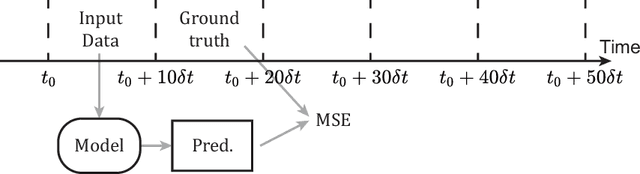
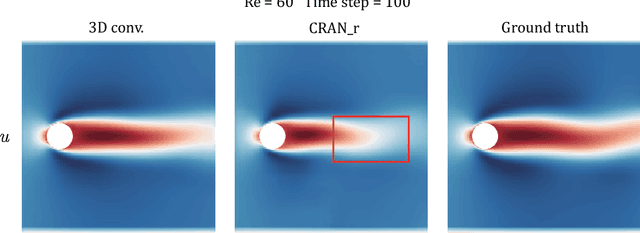
There is a critical need for efficient and reliable active flow control strategies to reduce drag and noise in aerospace and marine engineering applications. While traditional full-order models based on the Navier-Stokes equations are not feasible, advanced model reduction techniques can be inefficient for active control tasks, especially with strong non-linearity and convection-dominated phenomena. Using convolutional recurrent autoencoder network architectures, deep learning-based reduced-order models have been recently shown to be effective while performing several orders of magnitude faster than full-order simulations. However, these models encounter significant challenges outside the training data, limiting their effectiveness for active control and optimization tasks. In this study, we aim to improve the extrapolation capability by modifying network architecture and integrating coupled space-time physics as an implicit bias. Reduced-order models via deep learning generally employ decoupling in spatial and temporal dimensions, which can introduce modeling and approximation errors. To alleviate these errors, we propose a novel technique for learning coupled spatial-temporal correlation using a 3D convolution network. We assess the proposed technique against a standard encoder-propagator-decoder model and demonstrate a superior extrapolation performance. To demonstrate the effectiveness of 3D convolution network, we consider a benchmark problem of the flow past a circular cylinder at laminar flow conditions and use the spatio-temporal snapshots from the full-order simulations. Our proposed 3D convolution architecture accurately captures the velocity and pressure fields for varying Reynolds numbers. Compared to the standard encoder-propagator-decoder network, the spatio-temporal-based 3D convolution network improves the prediction range of Reynolds numbers outside of the training data.

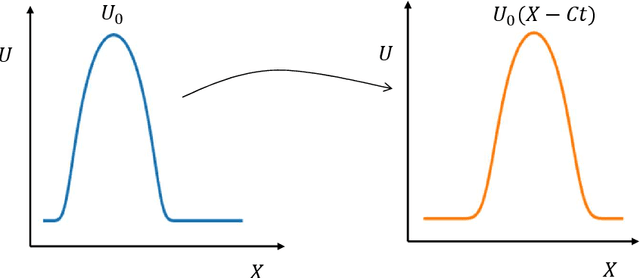
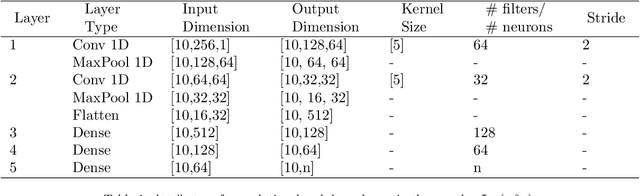
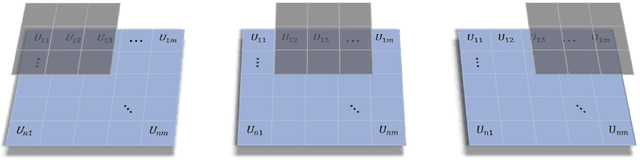
Learning Wave Propagation with Attention-Based Convolutional Recurrent Autoencoder Net

In this paper, we present an end-to-end attention-based convolutional recurrent autoencoder network (AB-CRAN) for data-driven modeling of wave propagation phenomena. To construct the low-dimensional learning model, we employ a denoising-based convolutional autoencoder from the full-order snapshots of wave propagation generated by solving hyperbolic partial differential equations. The proposed deep neural network architecture relies on the attention-based recurrent neural network (RNN) with long short-term memory (LSTM) cells for constructing the trajectory in the latent space. We assess the proposed AB-CRAN framework against the standard RNN-LSTM for the low-dimensional learning of wave propagation. To demonstrate the effectiveness of the AB-CRAN model, we consider three benchmark problems namely one-dimensional linear convection, nonlinear viscous Burgers, and two-dimensional Saint-Venant shallow water system. Using the time-series datasets from the benchmark problems, our novel AB-CRAN architecture accurately captures the wave amplitude and preserves the wave characteristics of the solution for long time horizons. The attention-based sequence-to-sequence network increases the time-horizon of prediction by five times compared to the standard RNN-LSTM. Denoising autoencoder further reduces the mean squared error of prediction and improves the generalization capability in the parameter space.