Learning Wave Propagation with Attention-Based Convolutional Recurrent Autoencoder Net

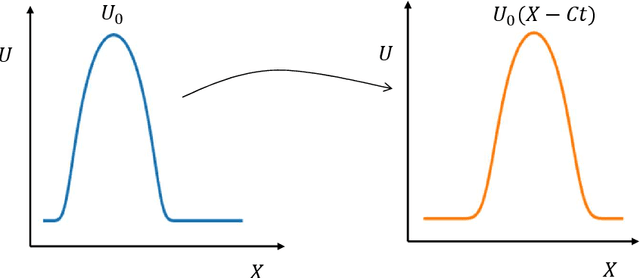
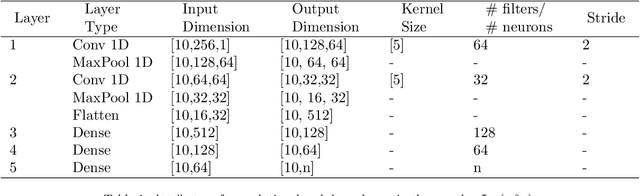
In this paper, we present an end-to-end attention-based convolutional recurrent autoencoder network (AB-CRAN) for data-driven modeling of wave propagation phenomena. To construct the low-dimensional learning model, we employ a denoising-based convolutional autoencoder from the full-order snapshots of wave propagation generated by solving hyperbolic partial differential equations. The proposed deep neural network architecture relies on the attention-based recurrent neural network (RNN) with long short-term memory (LSTM) cells for constructing the trajectory in the latent space. We assess the proposed AB-CRAN framework against the standard RNN-LSTM for the low-dimensional learning of wave propagation. To demonstrate the effectiveness of the AB-CRAN model, we consider three benchmark problems namely one-dimensional linear convection, nonlinear viscous Burgers, and two-dimensional Saint-Venant shallow water system. Using the time-series datasets from the benchmark problems, our novel AB-CRAN architecture accurately captures the wave amplitude and preserves the wave characteristics of the solution for long time horizons. The attention-based sequence-to-sequence network increases the time-horizon of prediction by five times compared to the standard RNN-LSTM. Denoising autoencoder further reduces the mean squared error of prediction and improves the generalization capability in the parameter space.