Harnessing Loss Decomposition for Long-Horizon Wave Predictions via Deep Neural Networks

Accurate prediction over long time horizons is crucial for modeling complex physical processes such as wave propagation. Although deep neural networks show promise for real-time forecasting, they often struggle with accumulating phase and amplitude errors as predictions extend over a long period. To address this issue, we propose a novel loss decomposition strategy that breaks down the loss into separate phase and amplitude components. This technique improves the long-term prediction accuracy of neural networks in wave propagation tasks by explicitly accounting for numerical errors, improving stability, and reducing error accumulation over extended forecasts.

Combined space-time reduced-order model with 3D deep convolution for extrapolating fluid dynamics

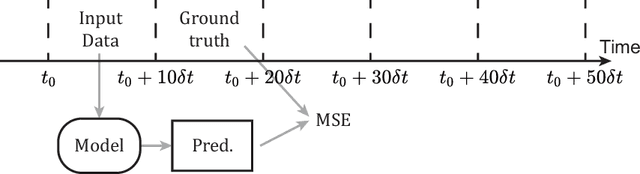
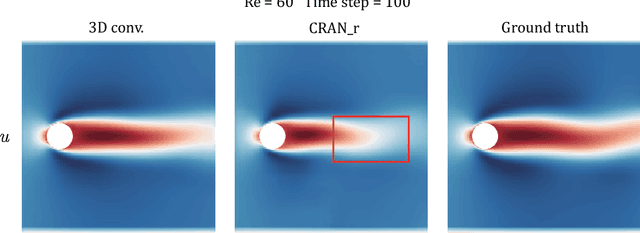
There is a critical need for efficient and reliable active flow control strategies to reduce drag and noise in aerospace and marine engineering applications. While traditional full-order models based on the Navier-Stokes equations are not feasible, advanced model reduction techniques can be inefficient for active control tasks, especially with strong non-linearity and convection-dominated phenomena. Using convolutional recurrent autoencoder network architectures, deep learning-based reduced-order models have been recently shown to be effective while performing several orders of magnitude faster than full-order simulations. However, these models encounter significant challenges outside the training data, limiting their effectiveness for active control and optimization tasks. In this study, we aim to improve the extrapolation capability by modifying network architecture and integrating coupled space-time physics as an implicit bias. Reduced-order models via deep learning generally employ decoupling in spatial and temporal dimensions, which can introduce modeling and approximation errors. To alleviate these errors, we propose a novel technique for learning coupled spatial-temporal correlation using a 3D convolution network. We assess the proposed technique against a standard encoder-propagator-decoder model and demonstrate a superior extrapolation performance. To demonstrate the effectiveness of 3D convolution network, we consider a benchmark problem of the flow past a circular cylinder at laminar flow conditions and use the spatio-temporal snapshots from the full-order simulations. Our proposed 3D convolution architecture accurately captures the velocity and pressure fields for varying Reynolds numbers. Compared to the standard encoder-propagator-decoder network, the spatio-temporal-based 3D convolution network improves the prediction range of Reynolds numbers outside of the training data.

Quasi-Monolithic Graph Neural Network for Fluid-Structure Interaction

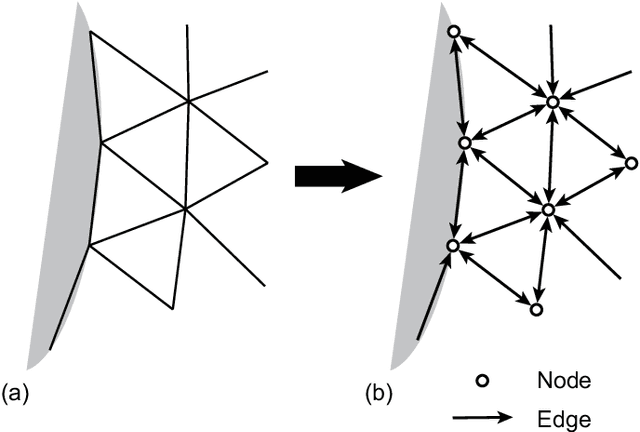
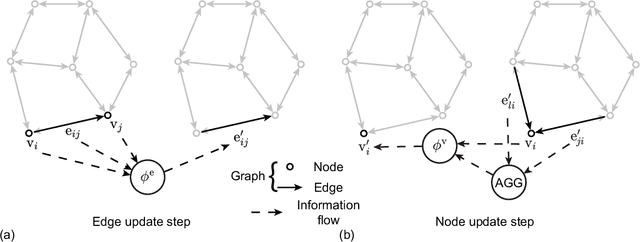
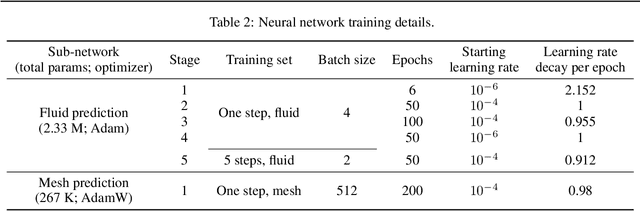
Using convolutional neural networks, deep learning-based reduced-order models have demonstrated great potential in accelerating the simulations of coupled fluid-structure systems for downstream optimization and control tasks. However, these networks have to operate on a uniform Cartesian grid due to the inherent restriction of convolutions, leading to difficulties in extracting fine physical details along a fluid-structure interface without excessive computational burden. In this work, we present a quasi-monolithic graph neural network framework for the reduced-order modelling of fluid-structure interaction systems. With the aid of an arbitrary Lagrangian-Eulerian formulation, the mesh and fluid states are evolved temporally with two sub-networks. The movement of the mesh is reduced to the evolution of several coefficients via proper orthogonal decomposition, and these coefficients are propagated through time via a multi-layer perceptron. A graph neural network is employed to predict the evolution of the fluid state based on the state of the whole system. The structural state is implicitly modelled by the movement of the mesh on the fluid-structure boundary; hence it makes the proposed data-driven methodology quasi-monolithic. The effectiveness of the proposed quasi-monolithic graph neural network architecture is assessed on a prototypical fluid-structure system of the flow around an elastically-mounted cylinder. We use the full-order flow snapshots and displacements as target physical data to learn and infer coupled fluid-structure dynamics. The proposed framework tracks the interface description and provides the state predictions during roll-out with acceptable accuracy. We also directly extract the lift and drag forces from the predicted fluid and mesh states, in contrast to existing convolution-based architectures.

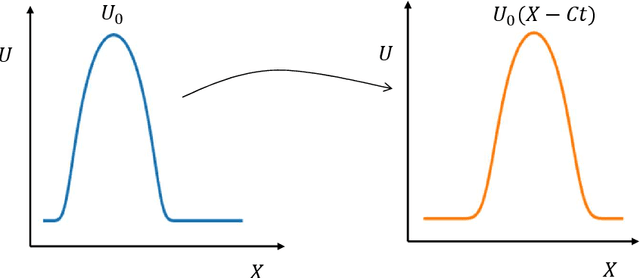
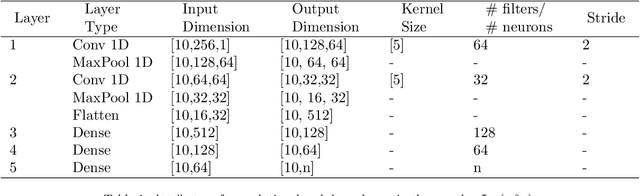
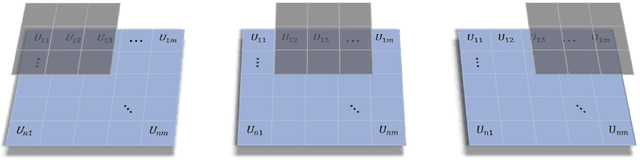
Learning Wave Propagation with Attention-Based Convolutional Recurrent Autoencoder Net

In this paper, we present an end-to-end attention-based convolutional recurrent autoencoder network (AB-CRAN) for data-driven modeling of wave propagation phenomena. To construct the low-dimensional learning model, we employ a denoising-based convolutional autoencoder from the full-order snapshots of wave propagation generated by solving hyperbolic partial differential equations. The proposed deep neural network architecture relies on the attention-based recurrent neural network (RNN) with long short-term memory (LSTM) cells for constructing the trajectory in the latent space. We assess the proposed AB-CRAN framework against the standard RNN-LSTM for the low-dimensional learning of wave propagation. To demonstrate the effectiveness of the AB-CRAN model, we consider three benchmark problems namely one-dimensional linear convection, nonlinear viscous Burgers, and two-dimensional Saint-Venant shallow water system. Using the time-series datasets from the benchmark problems, our novel AB-CRAN architecture accurately captures the wave amplitude and preserves the wave characteristics of the solution for long time horizons. The attention-based sequence-to-sequence network increases the time-horizon of prediction by five times compared to the standard RNN-LSTM. Denoising autoencoder further reduces the mean squared error of prediction and improves the generalization capability in the parameter space.