Rui Gao
LLM-Driven Scenario-Aware Planning for Autonomous Driving
Jan 29, 2026Abstract:Hybrid planner switching framework (HPSF) for autonomous driving needs to reconcile high-speed driving efficiency with safe maneuvering in dense traffic. Existing HPSF methods often fail to make reliable mode transitions or sustain efficient driving in congested environments, owing to heuristic scene recognition and low-frequency control updates. To address the limitation, this paper proposes LAP, a large language model (LLM) driven, adaptive planning method, which switches between high-speed driving in low-complexity scenes and precise driving in high-complexity scenes, enabling high qualities of trajectory generation through confined gaps. This is achieved by leveraging LLM for scene understanding and integrating its inference into the joint optimization of mode configuration and motion planning. The joint optimization is solved using tree-search model predictive control and alternating minimization. We implement LAP by Python in Robot Operating System (ROS). High-fidelity simulation results show that the proposed LAP outperforms other benchmarks in terms of both driving time and success rate.
DeepHalo: A Neural Choice Model with Controllable Context Effects
Jan 08, 2026Abstract:Modeling human decision-making is central to applications such as recommendation, preference learning, and human-AI alignment. While many classic models assume context-independent choice behavior, a large body of behavioral research shows that preferences are often influenced by the composition of the choice set itself -- a phenomenon known as the context effect or Halo effect. These effects can manifest as pairwise (first-order) or even higher-order interactions among the available alternatives. Recent models that attempt to capture such effects either focus on the featureless setting or, in the feature-based setting, rely on restrictive interaction structures or entangle interactions across all orders, which limits interpretability. In this work, we propose DeepHalo, a neural modeling framework that incorporates features while enabling explicit control over interaction order and principled interpretation of context effects. Our model enables systematic identification of interaction effects by order and serves as a universal approximator of context-dependent choice functions when specialized to a featureless setting. Experiments on synthetic and real-world datasets demonstrate strong predictive performance while providing greater transparency into the drivers of choice.
Sigma-MoE-Tiny Technical Report
Dec 19, 2025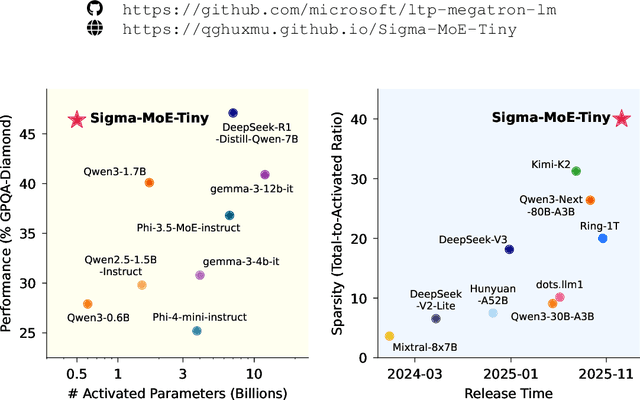

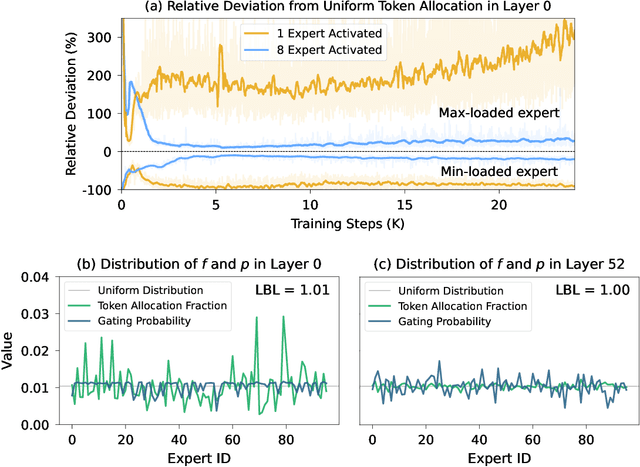
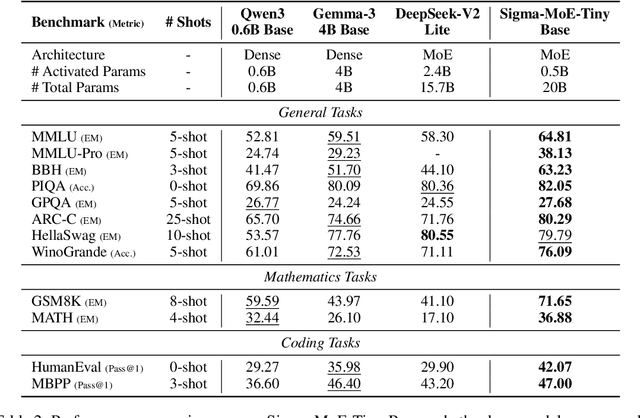
Abstract:Mixture-of-Experts (MoE) has emerged as a promising paradigm for foundation models due to its efficient and powerful scalability. In this work, we present Sigma-MoE-Tiny, an MoE language model that achieves the highest sparsity compared to existing open-source models. Sigma-MoE-Tiny employs fine-grained expert segmentation with up to 96 experts per layer, while activating only one expert for each token, resulting in 20B total parameters with just 0.5B activated. The major challenge introduced by such extreme sparsity lies in expert load balancing. We find that the widely-used load balancing loss tends to become ineffective in the lower layers under this setting. To address this issue, we propose a progressive sparsification schedule aiming to balance expert utilization and training stability. Sigma-MoE-Tiny is pre-trained on a diverse and high-quality corpus, followed by post-training to further unlock its capabilities. The entire training process remains remarkably stable, with no occurrence of irrecoverable loss spikes. Comprehensive evaluations reveal that, despite activating only 0.5B parameters, Sigma-MoE-Tiny achieves top-tier performance among counterparts of comparable or significantly larger scale. In addition, we provide an in-depth discussion of load balancing in highly sparse MoE models, offering insights for advancing sparsity in future MoE architectures. Project page: https://qghuxmu.github.io/Sigma-MoE-Tiny Code: https://github.com/microsoft/ltp-megatron-lm
SIGMA: An AI-Empowered Training Stack on Early-Life Hardware
Dec 15, 2025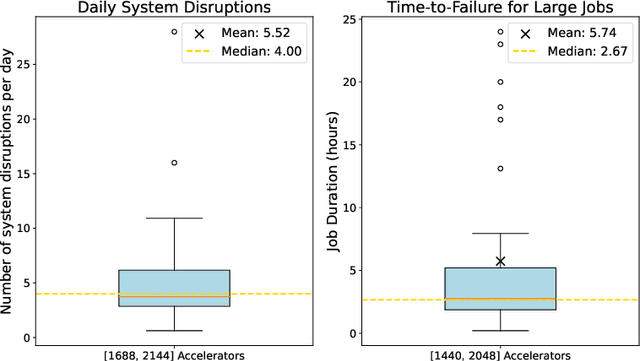

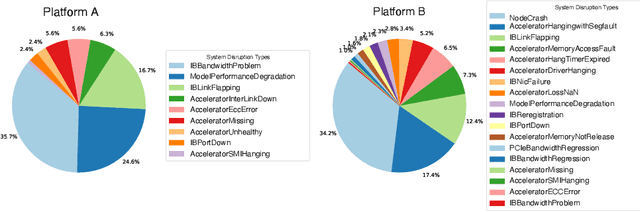

Abstract:An increasing variety of AI accelerators is being considered for large-scale training. However, enabling large-scale training on early-life AI accelerators faces three core challenges: frequent system disruptions and undefined failure modes that undermine reliability; numerical errors and training instabilities that threaten correctness and convergence; and the complexity of parallelism optimization combined with unpredictable local noise that degrades efficiency. To address these challenges, SIGMA is an open-source training stack designed to improve the reliability, stability, and efficiency of large-scale distributed training on early-life AI hardware. The core of this initiative is the LUCIA TRAINING PLATFORM (LTP), the system optimized for clusters with early-life AI accelerators. Since its launch in March 2025, LTP has significantly enhanced training reliability and operational productivity. Over the past five months, it has achieved an impressive 94.45% effective cluster accelerator utilization, while also substantially reducing node recycling and job-recovery times. Building on the foundation of LTP, the LUCIA TRAINING FRAMEWORK (LTF) successfully trained SIGMA-MOE, a 200B MoE model, using 2,048 AI accelerators. This effort delivered remarkable stability and efficiency outcomes, achieving 21.08% MFU, state-of-the-art downstream accuracy, and encountering only one stability incident over a 75-day period. Together, these advances establish SIGMA, which not only tackles the critical challenges of large-scale training but also establishes a new benchmark for AI infrastructure and platform innovation, offering a robust, cost-effective alternative to prevailing established accelerator stacks and significantly advancing AI capabilities and scalability. The source code of SIGMA is available at https://github.com/microsoft/LuciaTrainingPlatform.
Data-driven modeling of fluid flow around rotating structures with graph neural networks
Mar 28, 2025Abstract:Graph neural networks, recently introduced into the field of fluid flow surrogate modeling, have been successfully applied to model the temporal evolution of various fluid flow systems. Existing applications, however, are mostly restricted to cases where the domain is time-invariant. The present work extends the application of graph neural network-based modeling to fluid flow around structures rotating with respect to a certain axis. Specifically, we propose to apply a graph neural network-based surrogate modeling for fluid flow with the mesh corotating with the structure. Unlike conventional data-driven approaches that rely on structured Cartesian meshes, our framework operates on unstructured co-rotating meshes, enforcing rotation equivariance of the learned model by leveraging co-rotating polar (2D) and cylindrical (3D) coordinate systems. To model the pressure for systems without Dirichlet pressure boundaries, we propose a novel local directed pressure difference formulation that is invariant to the reference pressure point and value. For flow systems with large mesh sizes, we introduce a scheme to train the network in single or distributed graphics processing units by accumulating the backpropagated gradients from partitions of the mesh. The effectiveness of our proposed framework is examined on two test cases: (i) fluid flow in a 2D rotating mixer, and (ii) the flow past a 3D rotating cube. Our results show that the model achieves stable and accurate rollouts for over 2000 time steps in periodic regimes while capturing accurate short-term dynamics in chaotic flow regimes. In addition, the drag and lift force predictions closely match the CFD calculations, highlighting the potential of the framework for modeling both periodic and chaotic fluid flow around rotating structures.
FetalFlex: Anatomy-Guided Diffusion Model for Flexible Control on Fetal Ultrasound Image Synthesis
Mar 19, 2025Abstract:Fetal ultrasound (US) examinations require the acquisition of multiple planes, each providing unique diagnostic information to evaluate fetal development and screening for congenital anomalies. However, obtaining a comprehensive, multi-plane annotated fetal US dataset remains challenging, particularly for rare or complex anomalies owing to their low incidence and numerous subtypes. This poses difficulties in training novice radiologists and developing robust AI models, especially for detecting abnormal fetuses. In this study, we introduce a Flexible Fetal US image generation framework (FetalFlex) to address these challenges, which leverages anatomical structures and multimodal information to enable controllable synthesis of fetal US images across diverse planes. Specifically, FetalFlex incorporates a pre-alignment module to enhance controllability and introduces a repaint strategy to ensure consistent texture and appearance. Moreover, a two-stage adaptive sampling strategy is developed to progressively refine image quality from coarse to fine levels. We believe that FetalFlex is the first method capable of generating both in-distribution normal and out-of-distribution abnormal fetal US images, without requiring any abnormal data. Experiments on multi-center datasets demonstrate that FetalFlex achieved state-of-the-art performance across multiple image quality metrics. A reader study further confirms the close alignment of the generated results with expert visual assessments. Furthermore, synthetic images by FetalFlex significantly improve the performance of six typical deep models in downstream classification and anomaly detection tasks. Lastly, FetalFlex's anatomy-level controllable generation offers a unique advantage for anomaly simulation and creating paired or counterfactual data at the pixel level. The demo is available at: https://dyf1023.github.io/FetalFlex/.
H-SIREN: Improving implicit neural representations with hyperbolic periodic functions
Oct 07, 2024


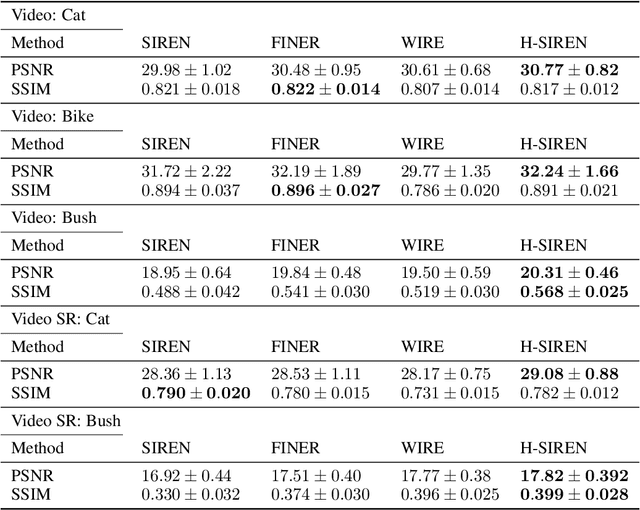
Abstract:Implicit neural representations (INR) have been recently adopted in various applications ranging from computer vision tasks to physics simulations by solving partial differential equations. Among existing INR-based works, multi-layer perceptrons with sinusoidal activation functions find widespread applications and are also frequently treated as a baseline for the development of better activation functions for INR applications. Recent investigations claim that the use of sinusoidal activation functions could be sub-optimal due to their limited supported frequency set as well as their tendency to generate over-smoothed solutions. We provide a simple solution to mitigate such an issue by changing the activation function at the first layer from $\sin(x)$ to $\sin(\sinh(2x))$. We demonstrate H-SIREN in various computer vision and fluid flow problems, where it surpasses the performance of several state-of-the-art INRs.
Regularization for Adversarial Robust Learning
Aug 22, 2024



Abstract:Despite the growing prevalence of artificial neural networks in real-world applications, their vulnerability to adversarial attacks remains a significant concern, which motivates us to investigate the robustness of machine learning models. While various heuristics aim to optimize the distributionally robust risk using the $\infty$-Wasserstein metric, such a notion of robustness frequently encounters computation intractability. To tackle the computational challenge, we develop a novel approach to adversarial training that integrates $\phi$-divergence regularization into the distributionally robust risk function. This regularization brings a notable improvement in computation compared with the original formulation. We develop stochastic gradient methods with biased oracles to solve this problem efficiently, achieving the near-optimal sample complexity. Moreover, we establish its regularization effects and demonstrate it is asymptotic equivalence to a regularized empirical risk minimization framework, by considering various scaling regimes of the regularization parameter and robustness level. These regimes yield gradient norm regularization, variance regularization, or a smoothed gradient norm regularization that interpolates between these extremes. We numerically validate our proposed method in supervised learning, reinforcement learning, and contextual learning and showcase its state-of-the-art performance against various adversarial attacks.
Data-driven Multistage Distributionally Robust Linear Optimization with Nested Distance
Jul 23, 2024



Abstract:We study multistage distributionally robust linear optimization, where the uncertainty set is defined as a ball of distribution centered at a scenario tree using the nested distance. The resulting minimax problem is notoriously difficult to solve due to its inherent non-convexity. In this paper, we demonstrate that, under mild conditions, the robust risk evaluation of a given policy can be expressed in an equivalent recursive form. Furthermore, assuming stagewise independence, we derive equivalent dynamic programming reformulations to find an optimal robust policy that is time-consistent and well-defined on unseen sample paths. Our reformulations reconcile two modeling frameworks: the multistage-static formulation (with nested distance) and the multistage-dynamic formulation (with one-period Wasserstein distance). Moreover, we identify tractable cases when the value functions can be computed efficiently using convex optimization techniques.
SFC: Achieve Accurate Fast Convolution under Low-precision Arithmetic
Jul 03, 2024Abstract:Fast convolution algorithms, including Winograd and FFT, can efficiently accelerate convolution operations in deep models. However, these algorithms depend on high-precision arithmetic to maintain inference accuracy, which conflicts with the model quantization. To resolve this conflict and further improve the efficiency of quantized convolution, we proposes SFC, a new algebra transform for fast convolution by extending the Discrete Fourier Transform (DFT) with symbolic computing, in which only additions are required to perform the transformation at specific transform points, avoiding the calculation of irrational number and reducing the requirement for precision. Additionally, we enhance convolution efficiency by introducing correction terms to convert invalid circular convolution outputs of the Fourier method into effective ones. The numerical error analysis is presented for the first time in this type of work and proves that our algorithms can provide a 3.68x multiplication reduction for 3x3 convolution, while the Winograd algorithm only achieves a 2.25x reduction with similarly low numerical errors. Experiments carried out on benchmarks and FPGA show that our new algorithms can further improve the computation efficiency of quantized models while maintaining accuracy, surpassing both the quantization-alone method and existing works on fast convolution quantization.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge