Rethinking Expert Trajectory Utilization in LLM Post-training

While effective post-training integrates Supervised Fine-Tuning (SFT) and Reinforcement Learning (RL), the optimal mechanism for utilizing expert trajectories remains unresolved. We propose the Plasticity-Ceiling Framework to theoretically ground this landscape, decomposing performance into foundational SFT performance and the subsequent RL plasticity. Through extensive benchmarking, we establish the Sequential SFT-then-RL pipeline as the superior standard, overcoming the stability deficits of synchronized approaches. Furthermore, we derive precise scaling guidelines: (1) Transitioning to RL at the SFT Stable or Mild Overfitting Sub-phase maximizes the final ceiling by securing foundational SFT performance without compromising RL plasticity; (2) Refuting ``Less is More'' in the context of SFT-then-RL scaling, we demonstrate that Data Scale determines the primary post-training potential, while Trajectory Difficulty acts as a performance multiplier; and (3) Identifying that the Minimum SFT Validation Loss serves as a robust indicator for selecting the expert trajectories that maximize the final performance ceiling. Our findings provide actionable guidelines for maximizing the value extracted from expert trajectories.

Point cloud-based registration and image fusion between cardiac SPECT MPI and CTA

A method was proposed for the point cloud-based registration and image fusion between cardiac single photon emission computed tomography (SPECT) myocardial perfusion images (MPI) and cardiac computed tomography angiograms (CTA). Firstly, the left ventricle (LV) epicardial regions (LVERs) in SPECT and CTA images were segmented by using different U-Net neural networks trained to generate the point clouds of the LV epicardial contours (LVECs). Secondly, according to the characteristics of cardiac anatomy, the special points of anterior and posterior interventricular grooves (APIGs) were manually marked in both SPECT and CTA image volumes. Thirdly, we developed an in-house program for coarsely registering the special points of APIGs to ensure a correct cardiac orientation alignment between SPECT and CTA images. Fourthly, we employed ICP, SICP or CPD algorithm to achieve a fine registration for the point clouds (together with the special points of APIGs) of the LV epicardial surfaces (LVERs) in SPECT and CTA images. Finally, the image fusion between SPECT and CTA was realized after the fine registration. The experimental results showed that the cardiac orientation was aligned well and the mean distance error of the optimal registration method (CPD with affine transform) was consistently less than 3 mm. The proposed method could effectively fuse the structures from cardiac CTA and SPECT functional images, and demonstrated a potential in assisting in accurate diagnosis of cardiac diseases by combining complementary advantages of the two imaging modalities.

Understanding and Generalizing Monotonic Proximity Graphs for Approximate Nearest Neighbor Search

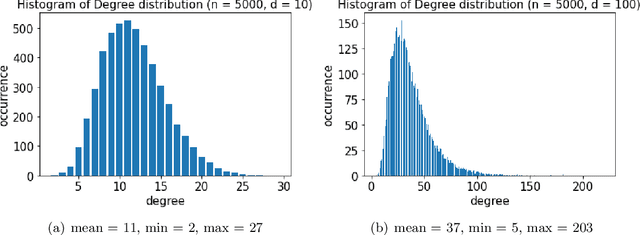
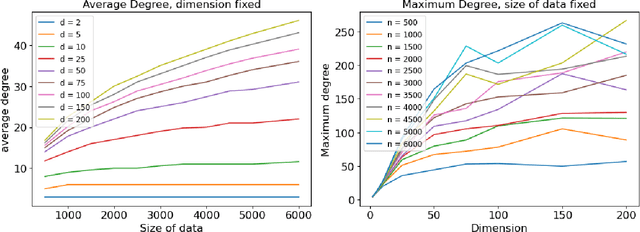
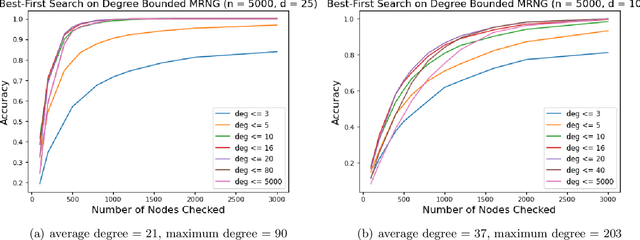
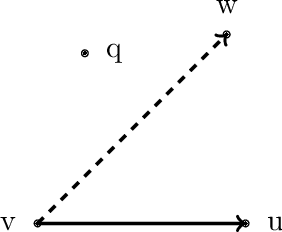
Graph-based algorithms have shown great empirical potential for the approximate nearest neighbor (ANN) search problem. Currently, graph-based ANN search algorithms are designed mainly using heuristics, whereas theoretical analysis of such algorithms is quite lacking. In this paper, we study a fundamental model of proximity graphs used in graph-based ANN search, called Monotonic Relative Neighborhood Graph (MRNG), from a theoretical perspective. We use mathematical proofs to explain why proximity graphs that are built based on MRNG tend to have good searching performance. We also run experiments on MRNG and graphs generalizing MRNG to obtain a deeper understanding of the model. Our experiments give guidance on how to approximate and generalize MRNG to build proximity graphs on a large scale. In addition, we discover and study a hidden structure of MRNG called conflicting nodes, and we give theoretical evidence how conflicting nodes could be used to improve ANN search methods that are based on MRNG.