Non-Convex Robust Hypothesis Testing using Sinkhorn Uncertainty Sets
Paper and Code
Mar 21, 2024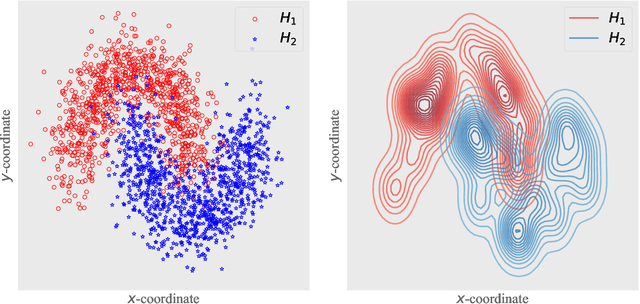

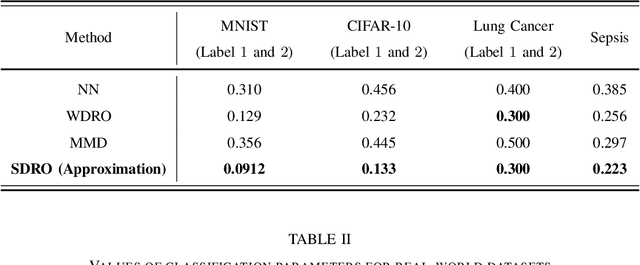

We present a new framework to address the non-convex robust hypothesis testing problem, wherein the goal is to seek the optimal detector that minimizes the maximum of worst-case type-I and type-II risk functions. The distributional uncertainty sets are constructed to center around the empirical distribution derived from samples based on Sinkhorn discrepancy. Given that the objective involves non-convex, non-smooth probabilistic functions that are often intractable to optimize, existing methods resort to approximations rather than exact solutions. To tackle the challenge, we introduce an exact mixed-integer exponential conic reformulation of the problem, which can be solved into a global optimum with a moderate amount of input data. Subsequently, we propose a convex approximation, demonstrating its superiority over current state-of-the-art methodologies in literature. Furthermore, we establish connections between robust hypothesis testing and regularized formulations of non-robust risk functions, offering insightful interpretations. Our numerical study highlights the satisfactory testing performance and computational efficiency of the proposed framework.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge