AdaSociety: An Adaptive Environment with Social Structures for Multi-Agent Decision-Making

Traditional interactive environments limit agents' intelligence growth with fixed tasks. Recently, single-agent environments address this by generating new tasks based on agent actions, enhancing task diversity. We consider the decision-making problem in multi-agent settings, where tasks are further influenced by social connections, affecting rewards and information access. However, existing multi-agent environments lack a combination of adaptive physical surroundings and social connections, hindering the learning of intelligent behaviors. To address this, we introduce AdaSociety, a customizable multi-agent environment featuring expanding state and action spaces, alongside explicit and alterable social structures. As agents progress, the environment adaptively generates new tasks with social structures for agents to undertake. In AdaSociety, we develop three mini-games showcasing distinct social structures and tasks. Initial results demonstrate that specific social structures can promote both individual and collective benefits, though current reinforcement learning and LLM-based algorithms show limited effectiveness in leveraging social structures to enhance performance. Overall, AdaSociety serves as a valuable research platform for exploring intelligence in diverse physical and social settings. The code is available at https://github.com/bigai-ai/AdaSociety.

Learning to Balance Altruism and Self-interest Based on Empathy in Mixed-Motive Games

Real-world multi-agent scenarios often involve mixed motives, demanding altruistic agents capable of self-protection against potential exploitation. However, existing approaches often struggle to achieve both objectives. In this paper, based on that empathic responses are modulated by inferred social relationships between agents, we propose LASE Learning to balance Altruism and Self-interest based on Empathy), a distributed multi-agent reinforcement learning algorithm that fosters altruistic cooperation through gifting while avoiding exploitation by other agents in mixed-motive games. LASE allocates a portion of its rewards to co-players as gifts, with this allocation adapting dynamically based on the social relationship -- a metric evaluating the friendliness of co-players estimated by counterfactual reasoning. In particular, social relationship measures each co-player by comparing the estimated $Q$-function of current joint action to a counterfactual baseline which marginalizes the co-player's action, with its action distribution inferred by a perspective-taking module. Comprehensive experiments are performed in spatially and temporally extended mixed-motive games, demonstrating LASE's ability to promote group collaboration without compromising fairness and its capacity to adapt policies to various types of interactive co-players.

Data-driven Multistage Distributionally Robust Linear Optimization with Nested Distance

We study multistage distributionally robust linear optimization, where the uncertainty set is defined as a ball of distribution centered at a scenario tree using the nested distance. The resulting minimax problem is notoriously difficult to solve due to its inherent non-convexity. In this paper, we demonstrate that, under mild conditions, the robust risk evaluation of a given policy can be expressed in an equivalent recursive form. Furthermore, assuming stagewise independence, we derive equivalent dynamic programming reformulations to find an optimal robust policy that is time-consistent and well-defined on unseen sample paths. Our reformulations reconcile two modeling frameworks: the multistage-static formulation (with nested distance) and the multistage-dynamic formulation (with one-period Wasserstein distance). Moreover, we identify tractable cases when the value functions can be computed efficiently using convex optimization techniques.

Efficient Adaptation in Mixed-Motive Environments via Hierarchical Opponent Modeling and Planning

Despite the recent successes of multi-agent reinforcement learning (MARL) algorithms, efficiently adapting to co-players in mixed-motive environments remains a significant challenge. One feasible approach is to hierarchically model co-players' behavior based on inferring their characteristics. However, these methods often encounter difficulties in efficient reasoning and utilization of inferred information. To address these issues, we propose Hierarchical Opponent modeling and Planning (HOP), a novel multi-agent decision-making algorithm that enables few-shot adaptation to unseen policies in mixed-motive environments. HOP is hierarchically composed of two modules: an opponent modeling module that infers others' goals and learns corresponding goal-conditioned policies, and a planning module that employs Monte Carlo Tree Search (MCTS) to identify the best response. Our approach improves efficiency by updating beliefs about others' goals both across and within episodes and by using information from the opponent modeling module to guide planning. Experimental results demonstrate that in mixed-motive environments, HOP exhibits superior few-shot adaptation capabilities when interacting with various unseen agents, and excels in self-play scenarios. Furthermore, the emergence of social intelligence during our experiments underscores the potential of our approach in complex multi-agent environments.

Learning While Dissipating Information: Understanding the Generalization Capability of SGLD

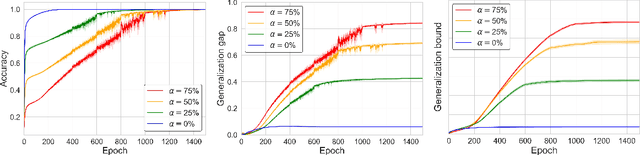
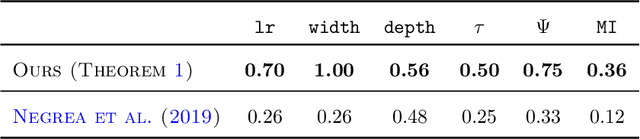
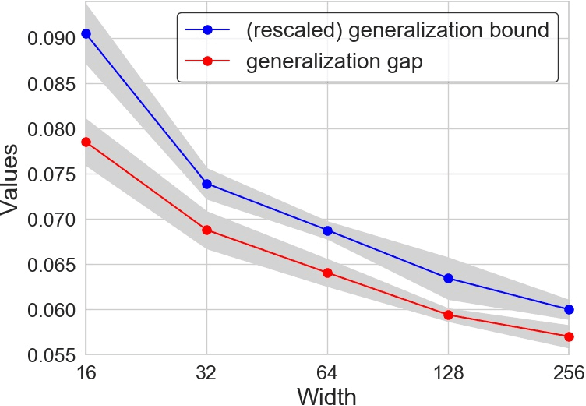
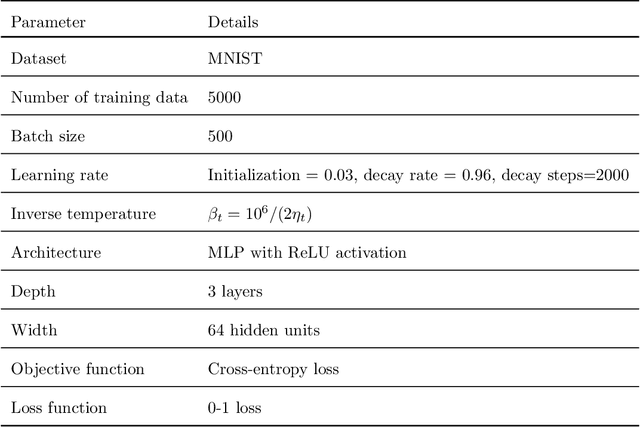
Understanding the generalization capability of learning algorithms is at the heart of statistical learning theory. In this paper, we investigate the generalization gap of stochastic gradient Langevin dynamics (SGLD), a widely used optimizer for training deep neural networks (DNNs). We derive an algorithm-dependent generalization bound by analyzing SGLD through an information-theoretic lens. Our analysis reveals an intricate trade-off between learning and information dissipation: SGLD learns from data by updating parameters at each iteration while dissipating information from early training stages. Our bound also involves the variance of gradients which captures a particular kind of "sharpness" of the loss landscape. The main proof techniques in this paper rely on strong data processing inequalities -- a fundamental concept in information theory -- and Otto-Villani's HWI inequality. Finally, we demonstrate our bound through numerical experiments, showing that it can predict the behavior of the true generalization gap.