Learning While Dissipating Information: Understanding the Generalization Capability of SGLD
Paper and Code
Feb 05, 2021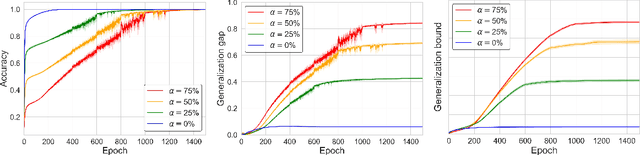
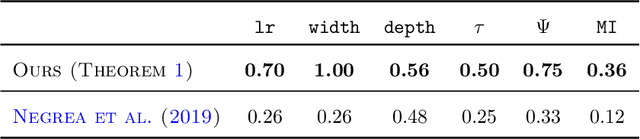
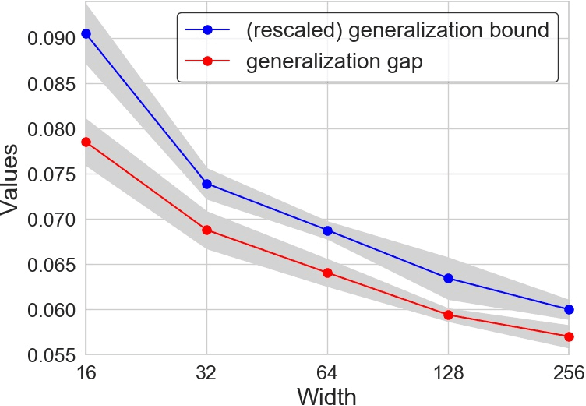
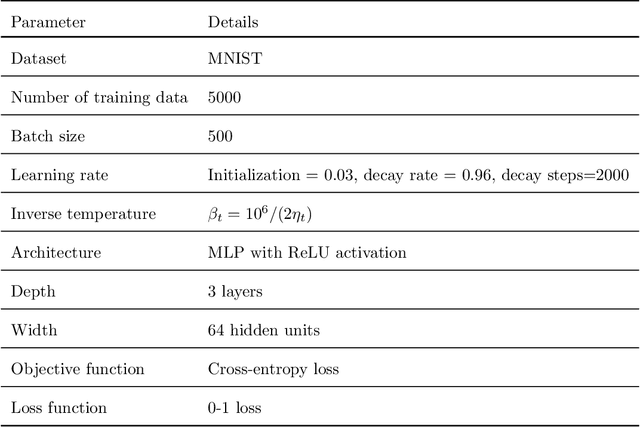
Understanding the generalization capability of learning algorithms is at the heart of statistical learning theory. In this paper, we investigate the generalization gap of stochastic gradient Langevin dynamics (SGLD), a widely used optimizer for training deep neural networks (DNNs). We derive an algorithm-dependent generalization bound by analyzing SGLD through an information-theoretic lens. Our analysis reveals an intricate trade-off between learning and information dissipation: SGLD learns from data by updating parameters at each iteration while dissipating information from early training stages. Our bound also involves the variance of gradients which captures a particular kind of "sharpness" of the loss landscape. The main proof techniques in this paper rely on strong data processing inequalities -- a fundamental concept in information theory -- and Otto-Villani's HWI inequality. Finally, we demonstrate our bound through numerical experiments, showing that it can predict the behavior of the true generalization gap.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge