Predicting Wave Dynamics using Deep Learning with Multistep Integration Inspired Attention and Physics-Based Loss Decomposition

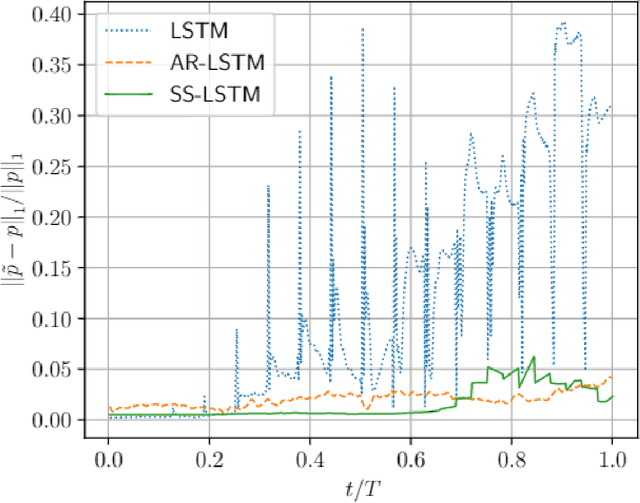
In this paper, we present a physics-based deep learning framework for data-driven prediction of wave propagation in fluid media. The proposed approach, termed Multistep Integration-Inspired Attention (MI2A), combines a denoising-based convolutional autoencoder for reduced latent representation with an attention-based recurrent neural network with long-short-term memory cells for time evolution of reduced coordinates. This proposed architecture draws inspiration from classical linear multistep methods to enhance stability and long-horizon accuracy in latent-time integration. Despite the efficiency of hybrid neural architectures in modeling wave dynamics, autoregressive predictions are often prone to accumulating phase and amplitude errors over time. To mitigate this issue within the MI2A framework, we introduce a novel loss decomposition strategy that explicitly separates the training loss function into distinct phase and amplitude components. We assess the performance of MI2A against two baseline reduced-order models trained with standard mean-squared error loss: a sequence-to-sequence recurrent neural network and a variant using Luong-style attention. To demonstrate the effectiveness of the MI2A model, we consider three benchmark wave propagation problems of increasing complexity, namely one-dimensional linear convection, the nonlinear viscous Burgers equation, and the two-dimensional Saint-Venant shallow water system. Our results demonstrate that the MI2A framework significantly improves the accuracy and stability of long-term predictions, accurately preserving wave amplitude and phase characteristics. Compared to the standard long-short term memory and attention-based models, MI2A-based deep learning exhibits superior generalization and temporal accuracy, making it a promising tool for real-time wave modeling.

Data-driven modeling of fluid flow around rotating structures with graph neural networks

Graph neural networks, recently introduced into the field of fluid flow surrogate modeling, have been successfully applied to model the temporal evolution of various fluid flow systems. Existing applications, however, are mostly restricted to cases where the domain is time-invariant. The present work extends the application of graph neural network-based modeling to fluid flow around structures rotating with respect to a certain axis. Specifically, we propose to apply a graph neural network-based surrogate modeling for fluid flow with the mesh corotating with the structure. Unlike conventional data-driven approaches that rely on structured Cartesian meshes, our framework operates on unstructured co-rotating meshes, enforcing rotation equivariance of the learned model by leveraging co-rotating polar (2D) and cylindrical (3D) coordinate systems. To model the pressure for systems without Dirichlet pressure boundaries, we propose a novel local directed pressure difference formulation that is invariant to the reference pressure point and value. For flow systems with large mesh sizes, we introduce a scheme to train the network in single or distributed graphics processing units by accumulating the backpropagated gradients from partitions of the mesh. The effectiveness of our proposed framework is examined on two test cases: (i) fluid flow in a 2D rotating mixer, and (ii) the flow past a 3D rotating cube. Our results show that the model achieves stable and accurate rollouts for over 2000 time steps in periodic regimes while capturing accurate short-term dynamics in chaotic flow regimes. In addition, the drag and lift force predictions closely match the CFD calculations, highlighting the potential of the framework for modeling both periodic and chaotic fluid flow around rotating structures.

H-SIREN: Improving implicit neural representations with hyperbolic periodic functions

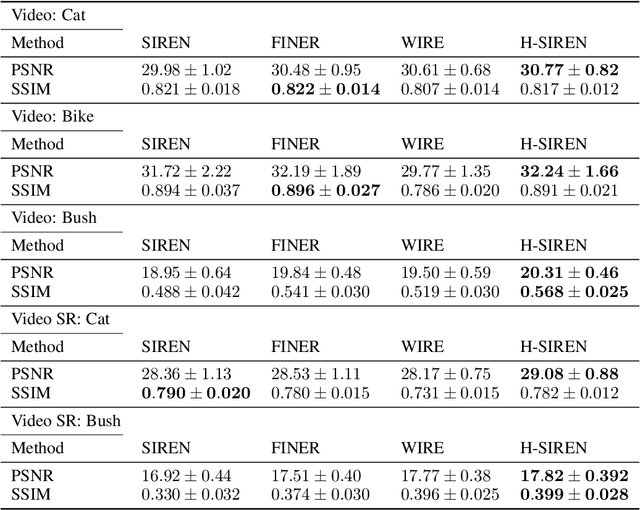
Implicit neural representations (INR) have been recently adopted in various applications ranging from computer vision tasks to physics simulations by solving partial differential equations. Among existing INR-based works, multi-layer perceptrons with sinusoidal activation functions find widespread applications and are also frequently treated as a baseline for the development of better activation functions for INR applications. Recent investigations claim that the use of sinusoidal activation functions could be sub-optimal due to their limited supported frequency set as well as their tendency to generate over-smoothed solutions. We provide a simple solution to mitigate such an issue by changing the activation function at the first layer from $\sin(x)$ to $\sin(\sinh(2x))$. We demonstrate H-SIREN in various computer vision and fluid flow problems, where it surpasses the performance of several state-of-the-art INRs.

Continual Learning of Range-Dependent Transmission Loss for Underwater Acoustic using Conditional Convolutional Neural Net

There is a significant need for precise and reliable forecasting of the far-field noise emanating from shipping vessels. Conventional full-order models based on the Navier-Stokes equations are unsuitable, and sophisticated model reduction methods may be ineffective for accurately predicting far-field noise in environments with seamounts and significant variations in bathymetry. Recent advances in reduced-order models, particularly those based on convolutional and recurrent neural networks, offer a faster and more accurate alternative. These models use convolutional neural networks to reduce data dimensions effectively. However, current deep-learning models face challenges in predicting wave propagation over long periods and for remote locations, often relying on auto-regressive prediction and lacking far-field bathymetry information. This research aims to improve the accuracy of deep-learning models for predicting underwater radiated noise in far-field scenarios. We propose a novel range-conditional convolutional neural network that incorporates ocean bathymetry data into the input. By integrating this architecture into a continual learning framework, we aim to generalize the model for varying bathymetry worldwide. To demonstrate the effectiveness of our approach, we analyze our model on several test cases and a benchmark scenario involving far-field prediction over Dickin's seamount in the Northeast Pacific. Our proposed architecture effectively captures transmission loss over a range-dependent, varying bathymetry profile. This architecture can be integrated into an adaptive management system for underwater radiated noise, providing real-time end-to-end mapping between near-field ship noise sources and received noise at the marine mammal's location.

Node-Element Hypergraph Message Passing for Fluid Dynamics Simulations

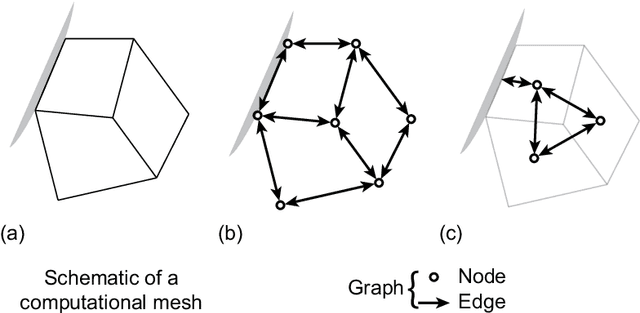
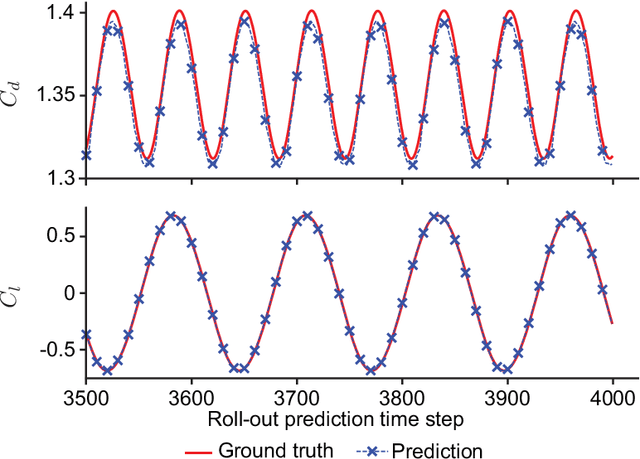
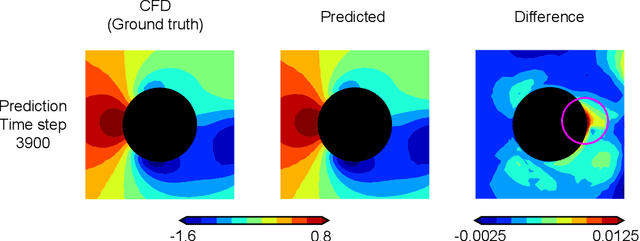
A recent trend in deep learning research features the application of graph neural networks for mesh-based continuum mechanics simulations. Most of these frameworks operate on graphs in which each edge connects two nodes. Inspired by the data connectivity in the finite element method, we connect the nodes by elements rather than edges, effectively forming a hypergraph. We implement a message-passing network on such a node-element hypergraph and explore the capability of the network for the modeling of fluid flow. The network is tested on two common benchmark problems, namely the fluid flow around a circular cylinder and airfoil configurations. The results show that such a message-passing network defined on the node-element hypergraph is able to generate more stable and accurate temporal roll-out predictions compared to the baseline generalized message-passing network defined on a normal graph. Along with adjustments in activation function and training loss, we expect this work to set a new strong baseline for future explorations of mesh-based fluid simulations with graph neural networks.

Convolutional recurrent autoencoder network for learning underwater ocean acoustics

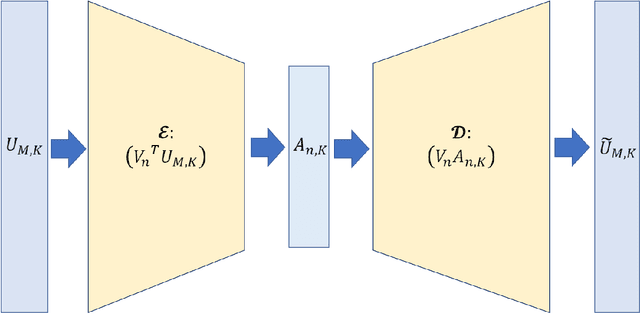
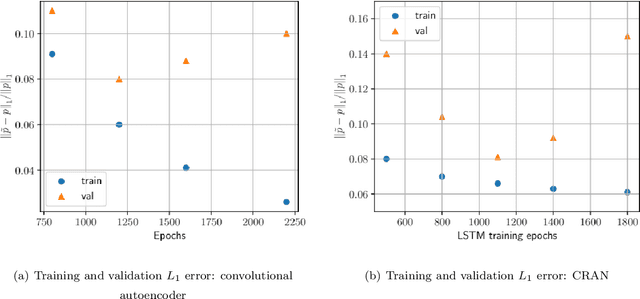
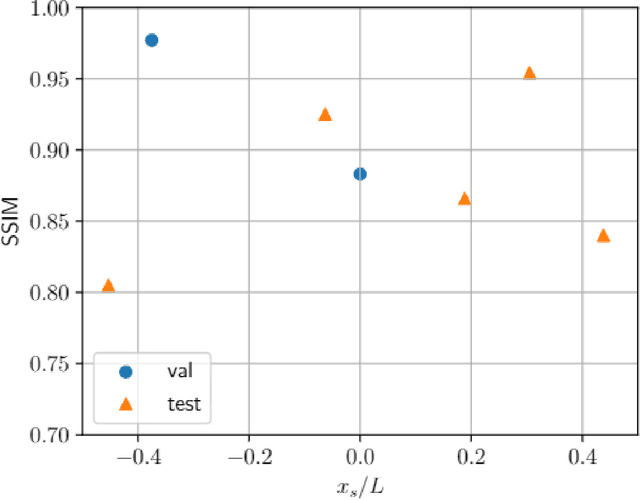
Underwater ocean acoustics is a complex physical phenomenon involving not only widely varying physical parameters and dynamical scales but also uncertainties in the ocean parameters. Thus, it is difficult to construct generalized physical models which can work in a broad range of situations. In this regard, we propose a convolutional recurrent autoencoder network (CRAN) architecture, which is a data-driven deep learning model for acoustic propagation. Being data-driven it is independent of how the data is obtained and can be employed for learning various ocean acoustic phenomena. The CRAN model can learn a reduced-dimensional representation of physical data and can predict the system evolution efficiently. Two cases of increasing complexity are considered to demonstrate the generalization ability of the CRAN. The first case is a one-dimensional wave propagation with spatially-varying discontinuous initial conditions. The second case corresponds to a far-field transmission loss distribution in a two-dimensional ocean domain with depth-dependent sources. For both cases, the CRAN can learn the essential elements of wave propagation physics such as characteristic patterns while predicting long-time system evolution with satisfactory accuracy. Such ability of the CRAN to learn complex ocean acoustics phenomena has the potential of real-time prediction for marine vessel decision-making and online control.

Deep convolutional neural network for shape optimization using level-set approach

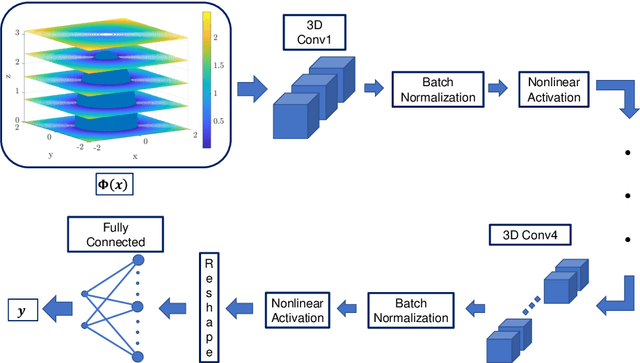
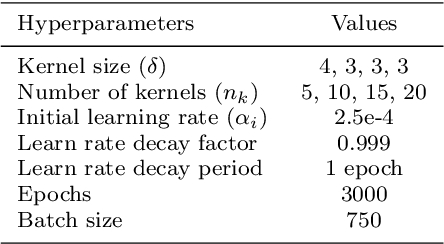
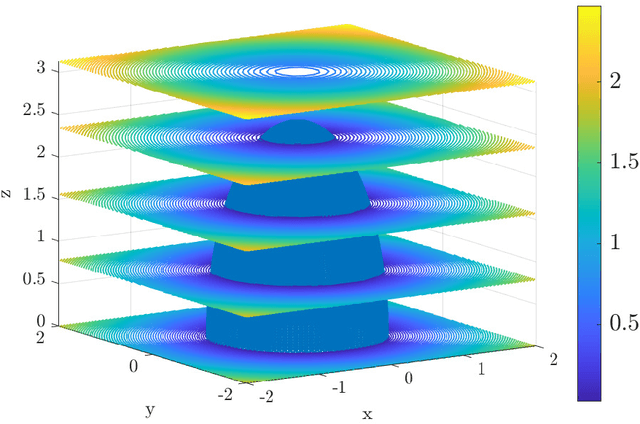
This article presents a reduced-order modeling methodology via deep convolutional neural networks (CNNs) for shape optimization applications. The CNN provides a nonlinear mapping between the shapes and their associated attributes while conserving the equivariance of these attributes to the shape translations. To implicitly represent complex shapes via a CNN-applicable Cartesian structured grid, a level-set method is employed. The CNN-based reduced-order model (ROM) is constructed in a completely data-driven manner thus well suited for non-intrusive applications. We demonstrate our ROM-based shape optimization framework on a gradient-based three-dimensional shape optimization problem to minimize the induced drag of a wing in low-fidelity potential flow. We show a good agreement between ROM-based optimal aerodynamic coefficients and their counterparts obtained via a potential flow solver. The predicted behavior of the optimized shape is consistent with theoretical predictions. We also present the learning mechanism of the deep CNN model in a physically interpretable manner. The CNN-ROM-based shape optimization algorithm exhibits significant computational efficiency compared to the full-order model-based online optimization applications. The proposed algorithm promises to develop a tractable DL-ROM-driven framework for shape optimization and adaptive morphing structures.

Kinematically consistent recurrent neural networks for learning inverse problems in wave propagation

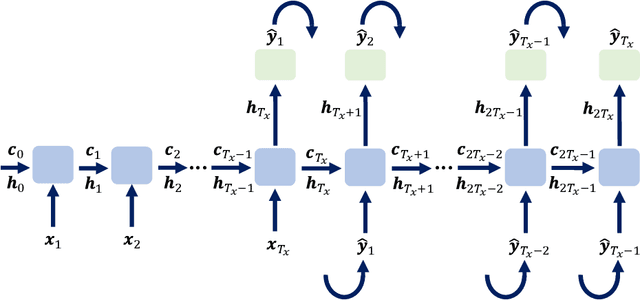
Although machine learning (ML) is increasingly employed recently for mechanistic problems, the black-box nature of conventional ML architectures lacks the physical knowledge to infer unforeseen input conditions. This implies both severe overfitting during a dearth of training data and inadequate physical interpretability, which motivates us to propose a new kinematically consistent, physics-based ML model. In particular, we attempt to perform physically interpretable learning of inverse problems in wave propagation without suffering overfitting restrictions. Towards this goal, we employ long short-term memory (LSTM) networks endowed with a physical, hyperparameter-driven regularizer, performing penalty-based enforcement of the characteristic geometries. Since these characteristics are the kinematical invariances of wave propagation phenomena, maintaining their structure provides kinematical consistency to the network. Even with modest training data, the kinematically consistent network can reduce the $L_1$ and $L_\infty$ error norms of the plain LSTM predictions by about 45% and 55%, respectively. It can also increase the horizon of the plain LSTM's forecasting by almost two times. To achieve this, an optimal range of the physical hyperparameter, analogous to an artificial bulk modulus, has been established through numerical experiments. The efficacy of the proposed method in alleviating overfitting, and the physical interpretability of the learning mechanism, are also discussed. Such an application of kinematically consistent LSTM networks for wave propagation learning is presented here for the first time.