Neil Farvolden
Deep convolutional neural network for shape optimization using level-set approach
Jan 24, 2022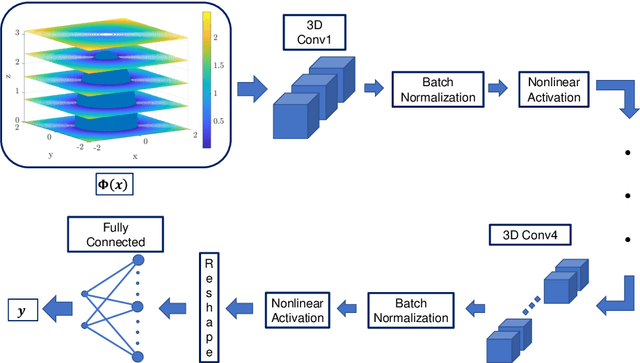
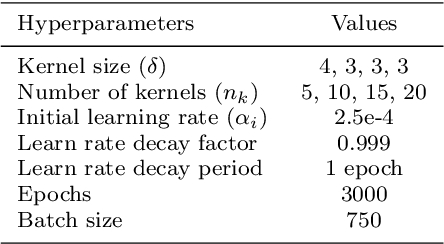
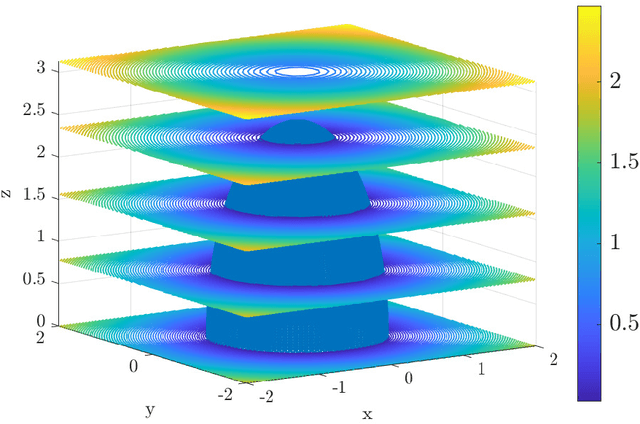

Abstract:This article presents a reduced-order modeling methodology via deep convolutional neural networks (CNNs) for shape optimization applications. The CNN provides a nonlinear mapping between the shapes and their associated attributes while conserving the equivariance of these attributes to the shape translations. To implicitly represent complex shapes via a CNN-applicable Cartesian structured grid, a level-set method is employed. The CNN-based reduced-order model (ROM) is constructed in a completely data-driven manner thus well suited for non-intrusive applications. We demonstrate our ROM-based shape optimization framework on a gradient-based three-dimensional shape optimization problem to minimize the induced drag of a wing in low-fidelity potential flow. We show a good agreement between ROM-based optimal aerodynamic coefficients and their counterparts obtained via a potential flow solver. The predicted behavior of the optimized shape is consistent with theoretical predictions. We also present the learning mechanism of the deep CNN model in a physically interpretable manner. The CNN-ROM-based shape optimization algorithm exhibits significant computational efficiency compared to the full-order model-based online optimization applications. The proposed algorithm promises to develop a tractable DL-ROM-driven framework for shape optimization and adaptive morphing structures.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge