Graph Neural Network for Stress Predictions in Stiffened Panels Under Uniform Loading

Machine learning (ML) and deep learning (DL) techniques have gained significant attention as reduced order models (ROMs) to computationally expensive structural analysis methods, such as finite element analysis (FEA). Graph neural network (GNN) is a particular type of neural network which processes data that can be represented as graphs. This allows for efficient representation of complex geometries that can change during conceptual design of a structure or a product. In this study, we propose a novel graph embedding technique for efficient representation of 3D stiffened panels by considering separate plate domains as vertices. This approach is considered using Graph Sampling and Aggregation (GraphSAGE) to predict stress distributions in stiffened panels with varying geometries. A comparison between a finite-element-vertex graph representation is conducted to demonstrate the effectiveness of the proposed approach. A comprehensive parametric study is performed to examine the effect of structural geometry on the prediction performance. Our results demonstrate the immense potential of graph neural networks with the proposed graph embedding method as robust reduced-order models for 3D structures.

Convolutional recurrent autoencoder network for learning underwater ocean acoustics

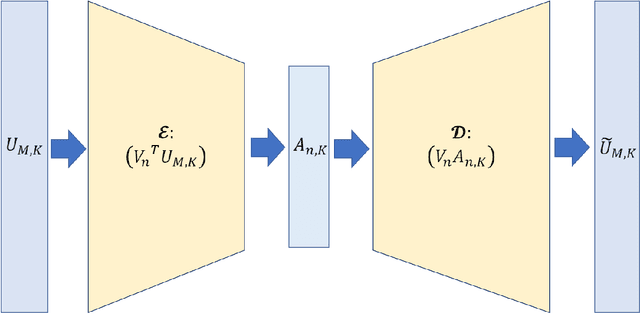
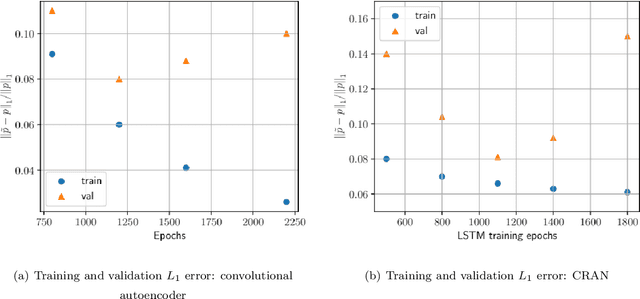
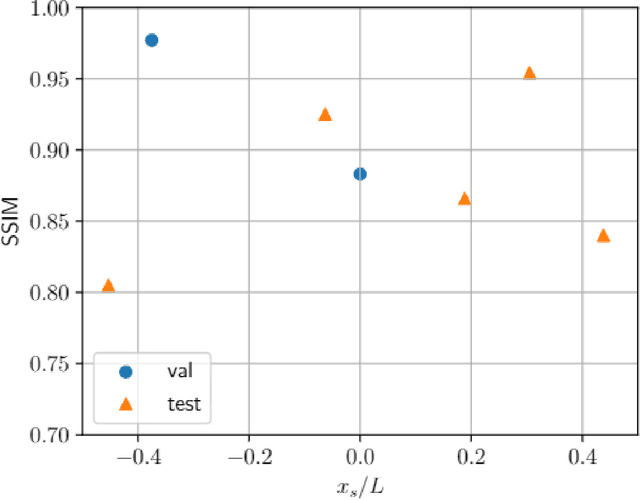
Underwater ocean acoustics is a complex physical phenomenon involving not only widely varying physical parameters and dynamical scales but also uncertainties in the ocean parameters. Thus, it is difficult to construct generalized physical models which can work in a broad range of situations. In this regard, we propose a convolutional recurrent autoencoder network (CRAN) architecture, which is a data-driven deep learning model for acoustic propagation. Being data-driven it is independent of how the data is obtained and can be employed for learning various ocean acoustic phenomena. The CRAN model can learn a reduced-dimensional representation of physical data and can predict the system evolution efficiently. Two cases of increasing complexity are considered to demonstrate the generalization ability of the CRAN. The first case is a one-dimensional wave propagation with spatially-varying discontinuous initial conditions. The second case corresponds to a far-field transmission loss distribution in a two-dimensional ocean domain with depth-dependent sources. For both cases, the CRAN can learn the essential elements of wave propagation physics such as characteristic patterns while predicting long-time system evolution with satisfactory accuracy. Such ability of the CRAN to learn complex ocean acoustics phenomena has the potential of real-time prediction for marine vessel decision-making and online control.

Deep convolutional neural network for shape optimization using level-set approach

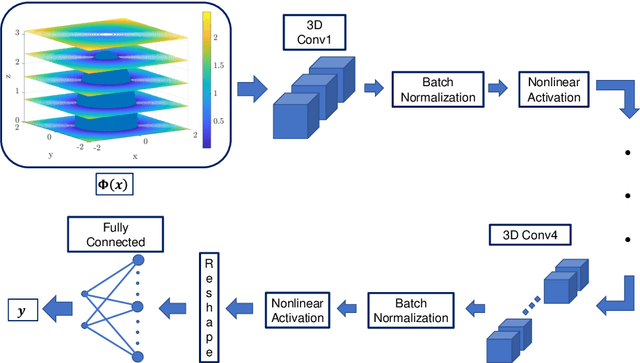
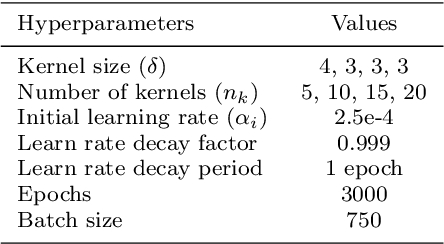
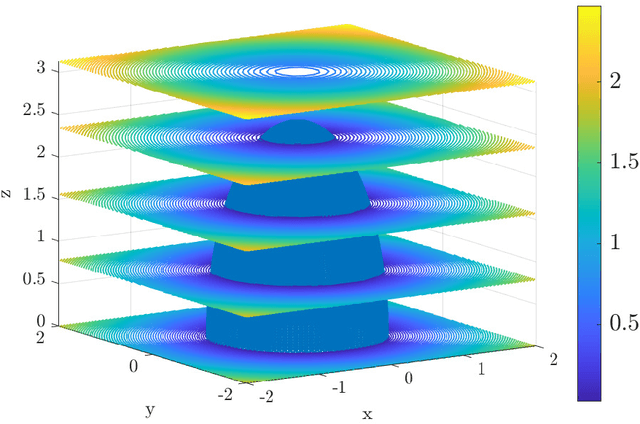
This article presents a reduced-order modeling methodology via deep convolutional neural networks (CNNs) for shape optimization applications. The CNN provides a nonlinear mapping between the shapes and their associated attributes while conserving the equivariance of these attributes to the shape translations. To implicitly represent complex shapes via a CNN-applicable Cartesian structured grid, a level-set method is employed. The CNN-based reduced-order model (ROM) is constructed in a completely data-driven manner thus well suited for non-intrusive applications. We demonstrate our ROM-based shape optimization framework on a gradient-based three-dimensional shape optimization problem to minimize the induced drag of a wing in low-fidelity potential flow. We show a good agreement between ROM-based optimal aerodynamic coefficients and their counterparts obtained via a potential flow solver. The predicted behavior of the optimized shape is consistent with theoretical predictions. We also present the learning mechanism of the deep CNN model in a physically interpretable manner. The CNN-ROM-based shape optimization algorithm exhibits significant computational efficiency compared to the full-order model-based online optimization applications. The proposed algorithm promises to develop a tractable DL-ROM-driven framework for shape optimization and adaptive morphing structures.

Kinematically consistent recurrent neural networks for learning inverse problems in wave propagation

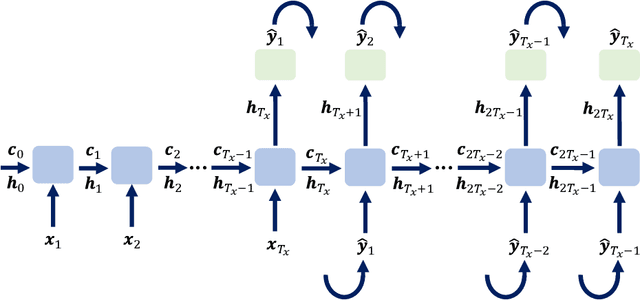
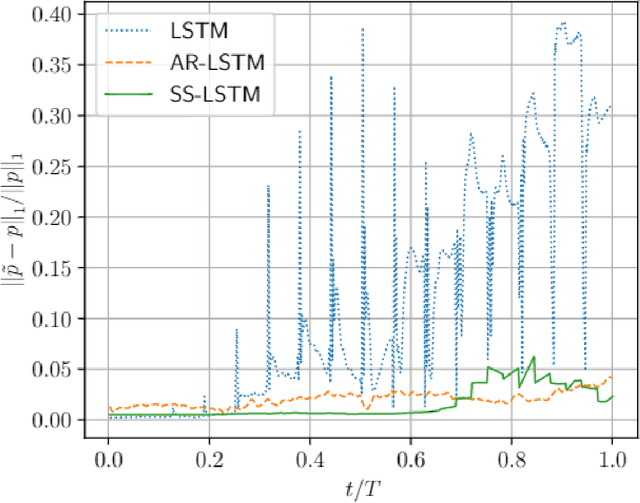
Although machine learning (ML) is increasingly employed recently for mechanistic problems, the black-box nature of conventional ML architectures lacks the physical knowledge to infer unforeseen input conditions. This implies both severe overfitting during a dearth of training data and inadequate physical interpretability, which motivates us to propose a new kinematically consistent, physics-based ML model. In particular, we attempt to perform physically interpretable learning of inverse problems in wave propagation without suffering overfitting restrictions. Towards this goal, we employ long short-term memory (LSTM) networks endowed with a physical, hyperparameter-driven regularizer, performing penalty-based enforcement of the characteristic geometries. Since these characteristics are the kinematical invariances of wave propagation phenomena, maintaining their structure provides kinematical consistency to the network. Even with modest training data, the kinematically consistent network can reduce the $L_1$ and $L_\infty$ error norms of the plain LSTM predictions by about 45% and 55%, respectively. It can also increase the horizon of the plain LSTM's forecasting by almost two times. To achieve this, an optimal range of the physical hyperparameter, analogous to an artificial bulk modulus, has been established through numerical experiments. The efficacy of the proposed method in alleviating overfitting, and the physical interpretability of the learning mechanism, are also discussed. Such an application of kinematically consistent LSTM networks for wave propagation learning is presented here for the first time.