Efficient machine-learning surrogates for large-scale geological carbon and energy storage

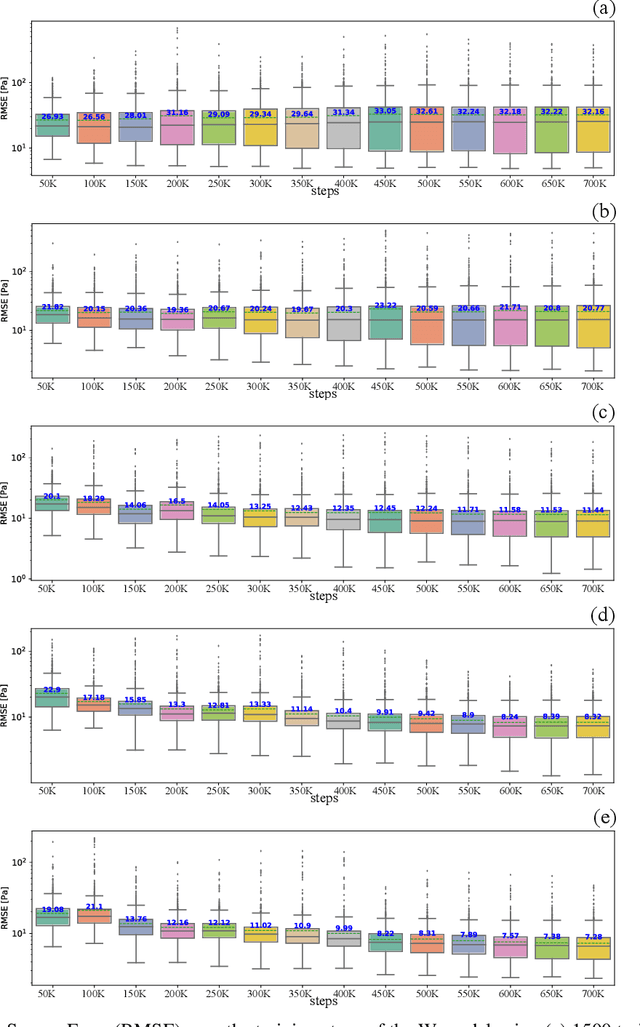
Geological carbon and energy storage are pivotal for achieving net-zero carbon emissions and addressing climate change. However, they face uncertainties due to geological factors and operational limitations, resulting in possibilities of induced seismic events or groundwater contamination. To overcome these challenges, we propose a specialized machine-learning (ML) model to manage extensive reservoir models efficiently. While ML approaches hold promise for geological carbon storage, the substantial computational resources required for large-scale analysis are the obstacle. We've developed a method to reduce the training cost for deep neural operator models, using domain decomposition and a topology embedder to link spatio-temporal points. This approach allows accurate predictions within the model's domain, even for untrained data, enhancing ML efficiency for large-scale geological storage applications.

Progressive reduced order modeling: empowering data-driven modeling with selective knowledge transfer

Data-driven modeling can suffer from a constant demand for data, leading to reduced accuracy and impractical for engineering applications due to the high cost and scarcity of information. To address this challenge, we propose a progressive reduced order modeling framework that minimizes data cravings and enhances data-driven modeling's practicality. Our approach selectively transfers knowledge from previously trained models through gates, similar to how humans selectively use valuable knowledge while ignoring unuseful information. By filtering relevant information from previous models, we can create a surrogate model with minimal turnaround time and a smaller training set that can still achieve high accuracy. We have tested our framework in several cases, including transport in porous media, gravity-driven flow, and finite deformation in hyperelastic materials. Our results illustrate that retaining information from previous models and utilizing a valuable portion of that knowledge can significantly improve the accuracy of the current model. We have demonstrated the importance of progressive knowledge transfer and its impact on model accuracy with reduced training samples. For instance, our framework with four parent models outperforms the no-parent counterpart trained on data nine times larger. Our research unlocks data-driven modeling's potential for practical engineering applications by mitigating the data scarcity issue. Our proposed framework is a significant step toward more efficient and cost-effective data-driven modeling, fostering advancements across various fields.

Reduced order modeling with Barlow Twins self-supervised learning: Navigating the space between linear and nonlinear solution manifolds

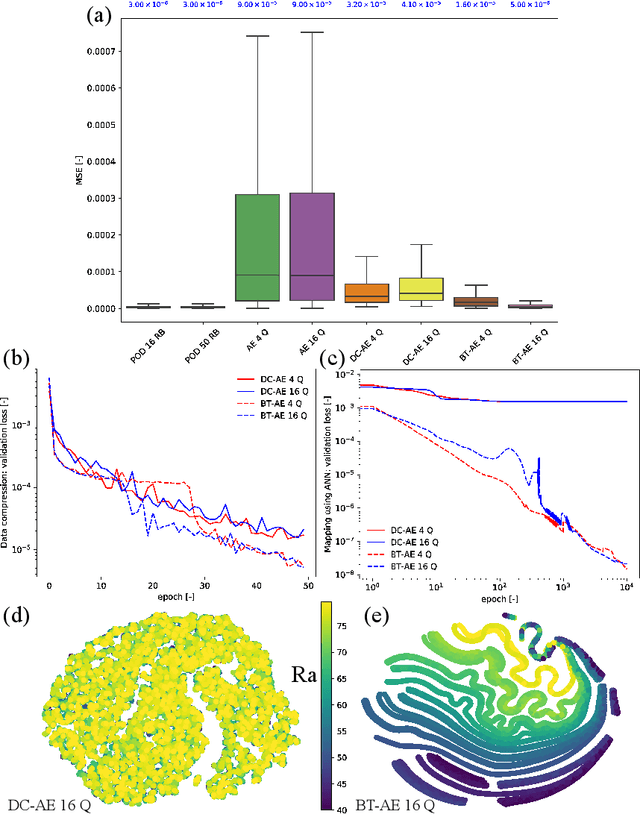
We propose a unified data-driven reduced order model (ROM) that bridges the performance gap between linear and nonlinear manifold approaches. Deep learning ROM (DL-ROM) using deep-convolutional autoencoders (DC-AE) has been shown to capture nonlinear solution manifolds but fails to perform adequately when linear subspace approaches such as proper orthogonal decomposition (POD) would be optimal. Besides, most DL-ROM models rely on convolutional layers, which might limit its application to only a structured mesh. The proposed framework in this study relies on the combination of an autoencoder (AE) and Barlow Twins (BT) self-supervised learning, where BT maximizes the information content of the embedding with the latent space through a joint embedding architecture. Through a series of benchmark problems of natural convection in porous media, BT-AE performs better than the previous DL-ROM framework by providing comparable results to POD-based approaches for problems where the solution lies within a linear subspace as well as DL-ROM autoencoder-based techniques where the solution lies on a nonlinear manifold; consequently, bridges the gap between linear and nonlinear reduced manifolds. Furthermore, this BT-AE framework can operate on unstructured meshes, which provides flexibility in its application to standard numerical solvers, on-site measurements, experimental data, or a combination of these sources.

A framework for data-driven solution and parameter estimation of PDEs using conditional generative adversarial networks

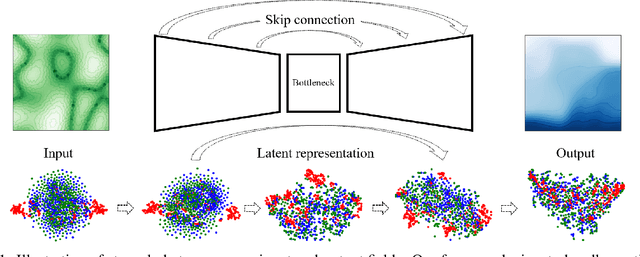
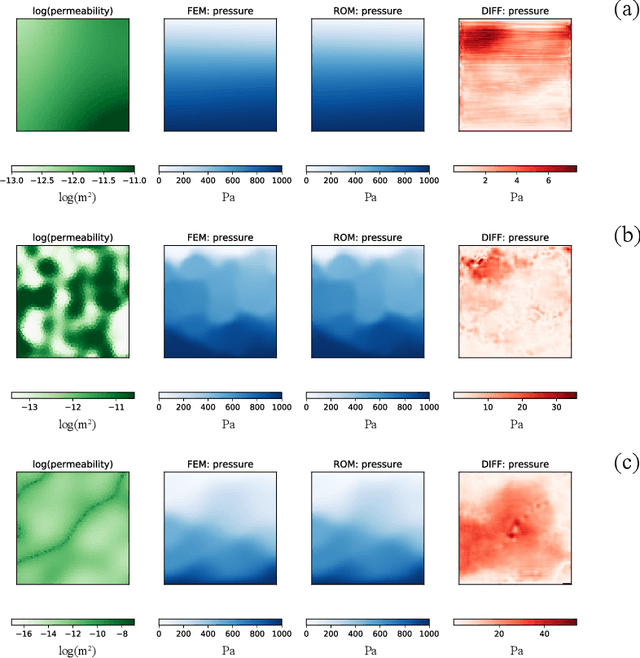
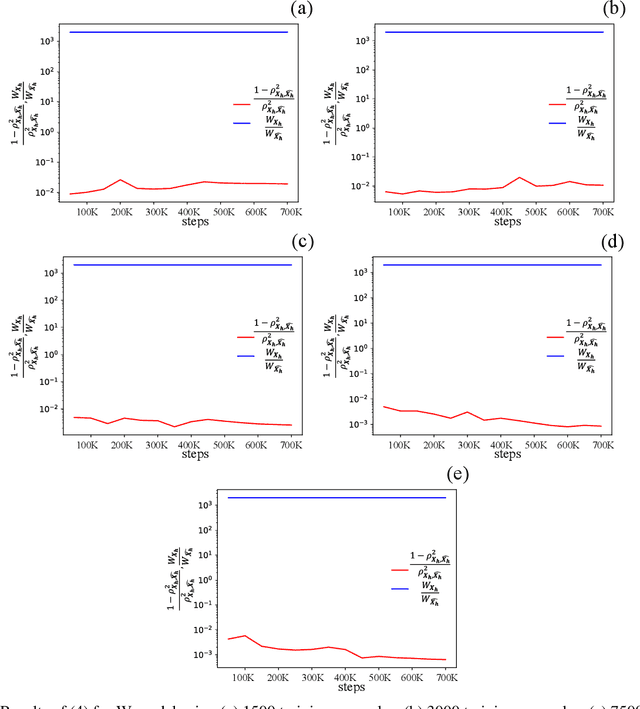
This work is the first to employ and adapt the image-to-image translation concept based on conditional generative adversarial networks (cGAN) towards learning a forward and an inverse solution operator of partial differential equations (PDEs). Even though the proposed framework could be applied as a surrogate model for the solution of any PDEs, here we focus on steady-state solutions of coupled hydro-mechanical processes in heterogeneous porous media. Strongly heterogeneous material properties, which translate to the heterogeneity of coefficients of the PDEs and discontinuous features in the solutions, require specialized techniques for the forward and inverse solution of these problems. Additionally, parametrization of the spatially heterogeneous coefficients is excessively difficult by using standard reduced order modeling techniques. In this work, we overcome these challenges by employing the image-to-image translation concept to learn the forward and inverse solution operators and utilize a U-Net generator and a patch-based discriminator. Our results show that the proposed data-driven reduced order model has competitive predictive performance capabilities in accuracy and computational efficiency as well as training time requirements compared to state-of-the-art data-driven methods for both forward and inverse problems.

Physics-informed Neural Networks for Solving Inverse Problems of Nonlinear Biot's Equations: Batch Training

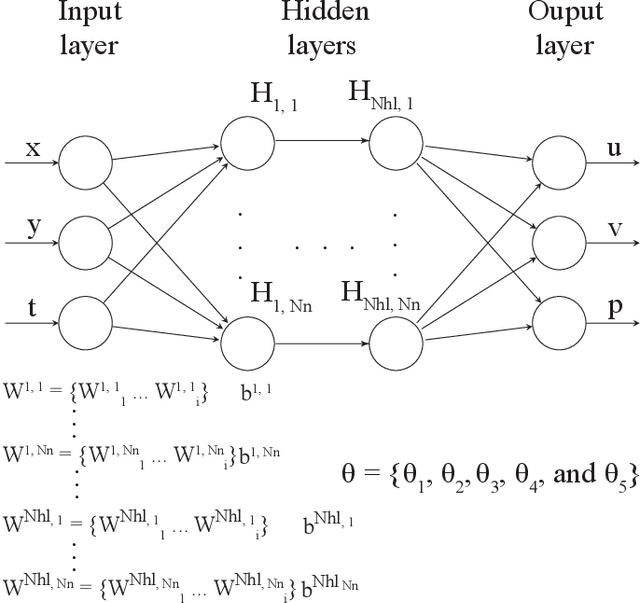
In biomedical engineering, earthquake prediction, and underground energy harvesting, it is crucial to indirectly estimate the physical properties of porous media since the direct measurement of those are usually impractical/prohibitive. Here we apply the physics-informed neural networks to solve the inverse problem with regard to the nonlinear Biot's equations. Specifically, we consider batch training and explore the effect of different batch sizes. The results show that training with small batch sizes, i.e., a few examples per batch, provides better approximations (lower percentage error) of the physical parameters than using large batches or the full batch. The increased accuracy of the physical parameters, comes at the cost of longer training time. Specifically, we find the size should not be too small since a very small batch size requires a very long training time without a corresponding improvement in estimation accuracy. We find that a batch size of 8 or 32 is a good compromise, which is also robust to additive noise in the data. The learning rate also plays an important role and should be used as a hyperparameter.

Physics-informed Neural Networks for Solving Nonlinear Diffusivity and Biot's equations

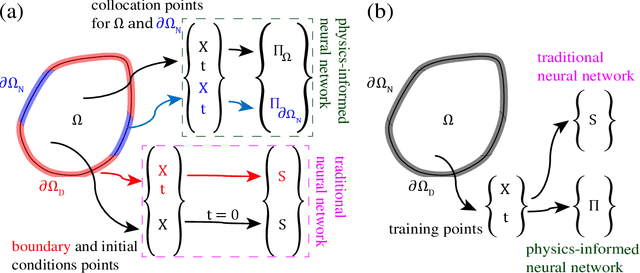
This paper presents the potential of applying physics-informed neural networks for solving nonlinear multiphysics problems, which are essential to many fields such as biomedical engineering, earthquake prediction, and underground energy harvesting. Specifically, we investigate how to extend the methodology of physics-informed neural networks to solve both the forward and inverse problems in relation to the nonlinear diffusivity and Biot's equations. We explore the accuracy of the physics-informed neural networks with different training example sizes and choices of hyperparameters. The impacts of the stochastic variations between various training realizations are also investigated. In the inverse case, we also study the effects of noisy measurements. Furthermore, we address the challenge of selecting the hyperparameters of the inverse model and illustrate how this challenge is linked to the hyperparameters selection performed for the forward one.