Multisource Semisupervised Adversarial Domain Generalization Network for Cross-Scene Sea\textendash Land Clutter Classification

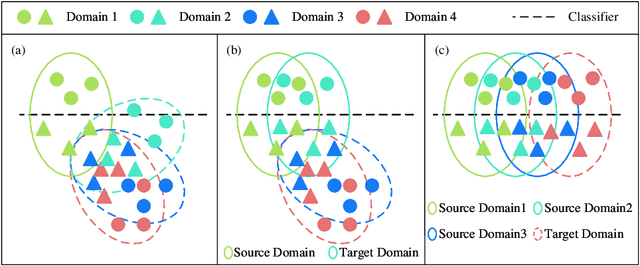
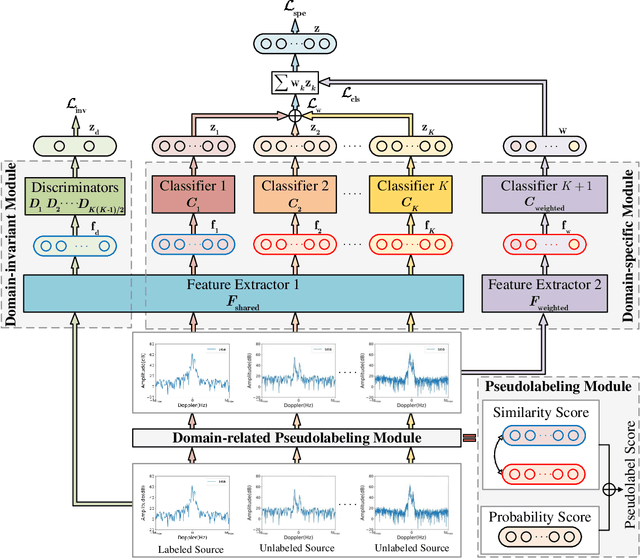
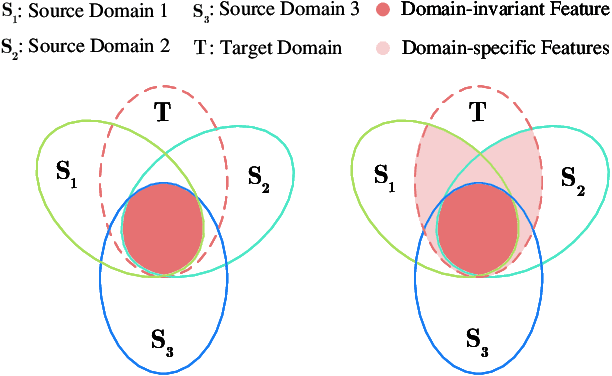
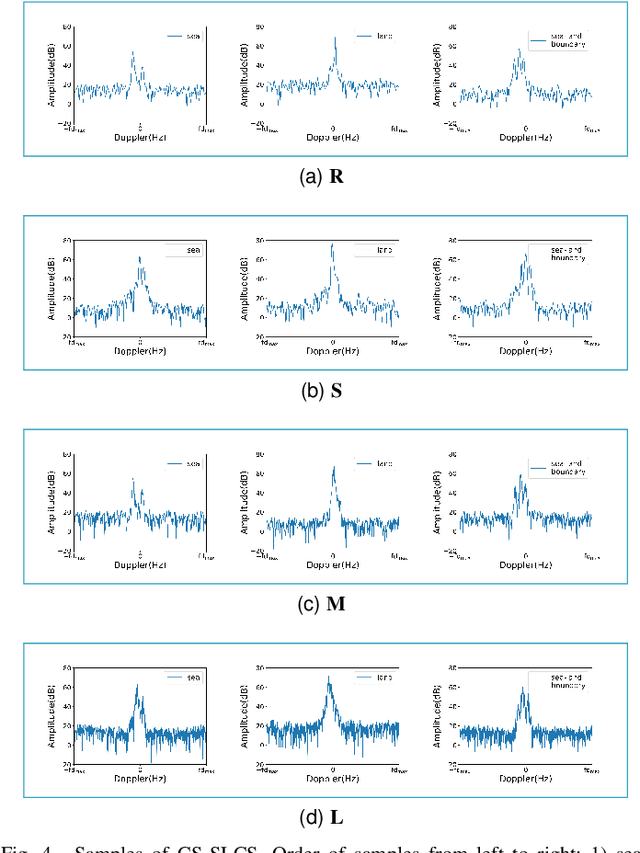
Deep learning (DL)-based sea\textendash land clutter classification for sky-wave over-the-horizon-radar (OTHR) has become a novel research topic. In engineering applications, real-time predictions of sea\textendash land clutter with existing distribution discrepancies are crucial. To solve this problem, this article proposes a novel Multisource Semisupervised Adversarial Domain Generalization Network (MSADGN) for cross-scene sea\textendash land clutter classification. MSADGN can extract domain-invariant and domain-specific features from one labeled source domain and multiple unlabeled source domains, and then generalize these features to an arbitrary unseen target domain for real-time prediction of sea\textendash land clutter. Specifically, MSADGN consists of three modules: domain-related pseudolabeling module, domain-invariant module, and domain-specific module. The first module introduces an improved pseudolabel method called domain-related pseudolabel, which is designed to generate reliable pseudolabels to fully exploit unlabeled source domains. The second module utilizes a generative adversarial network (GAN) with a multidiscriminator to extract domain-invariant features, to enhance the model's transferability in the target domain. The third module employs a parallel multiclassifier branch to extract domain-specific features, to enhance the model's discriminability in the target domain. The effectiveness of our method is validated in twelve domain generalizations (DG) scenarios. Meanwhile, we selected 10 state-of-the-art DG methods for comparison. The experimental results demonstrate the superiority of our method.

A Sea-Land Clutter Classification Framework for Over-the-Horizon-Radar Based on Weighted Loss Semi-supervised GAN

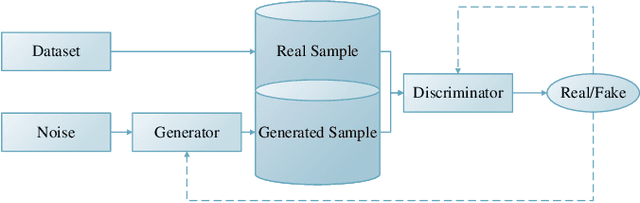
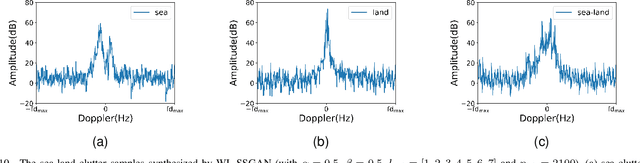
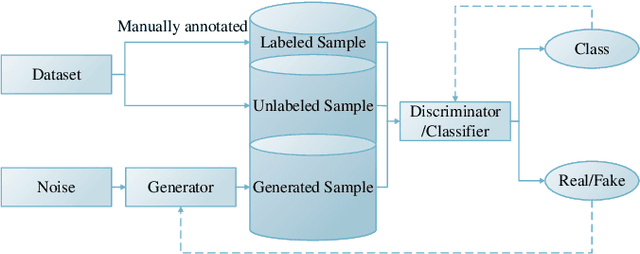
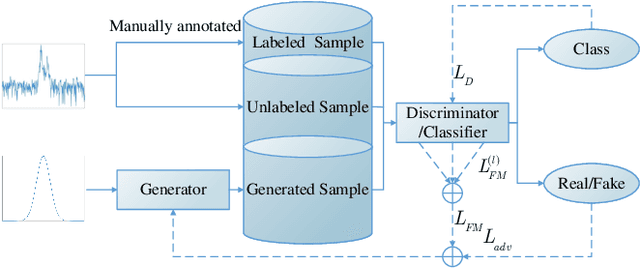
Deep convolutional neural network has made great achievements in sea-land clutter classification for over-the-horizon-radar (OTHR). The premise is that a large number of labeled training samples must be provided for a sea-land clutter classifier. In practical engineering applications, it is relatively easy to obtain label-free sea-land clutter samples. However, the labeling process is extremely cumbersome and requires expertise in the field of OTHR. To solve this problem, we propose an improved generative adversarial network, namely weighted loss semi-supervised generative adversarial network (WL-SSGAN). Specifically, we propose a joint feature matching loss by weighting the middle layer features of the discriminator of semi-supervised generative adversarial network. Furthermore, we propose the weighted loss of WL-SSGAN by linearly weighting standard adversarial loss and joint feature matching loss. The semi-supervised classification performance of WL-SSGAN is evaluated on a sea-land clutter dataset. The experimental results show that WL-SSGAN can improve the performance of the fully supervised classifier with only a small number of labeled samples by utilizing a large number of unlabeled sea-land clutter samples. Further, the proposed weighted loss is superior to both the adversarial loss and the feature matching loss. Additionally, we compare WL-SSGAN with conventional semi-supervised classification methods and demonstrate that WL-SSGAN achieves the highest classification accuracy.

A heteroencoder architecture for prediction of failure locations in porous metals using variational inference

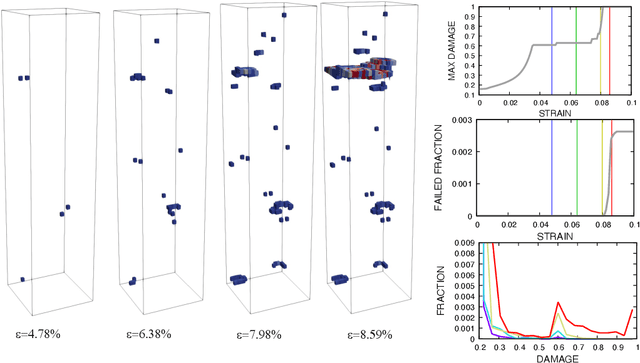
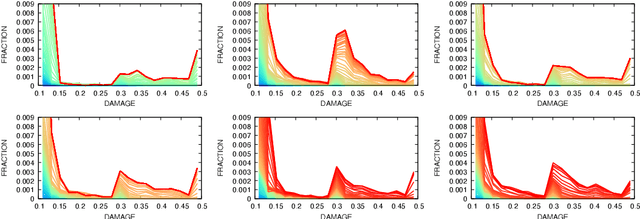
In this work we employ an encoder-decoder convolutional neural network to predict the failure locations of porous metal tension specimens based only on their initial porosities. The process we model is complex, with a progression from initial void nucleation, to saturation, and ultimately failure. The objective of predicting failure locations presents an extreme case of class imbalance since most of the material in the specimens do not fail. In response to this challenge, we develop and demonstrate the effectiveness of data- and loss-based regularization methods. Since there is considerable sensitivity of the failure location to the particular configuration of voids, we also use variational inference to provide uncertainties for the neural network predictions. We connect the deterministic and Bayesian convolutional neural networks at a theoretical level to explain how variational inference regularizes the training and predictions. We demonstrate that the resulting predicted variances are effective in ranking the locations that are most likely to fail in any given specimen.

Using Uncertainty in Deep Learning Reconstruction for Cone-Beam CT of the Brain

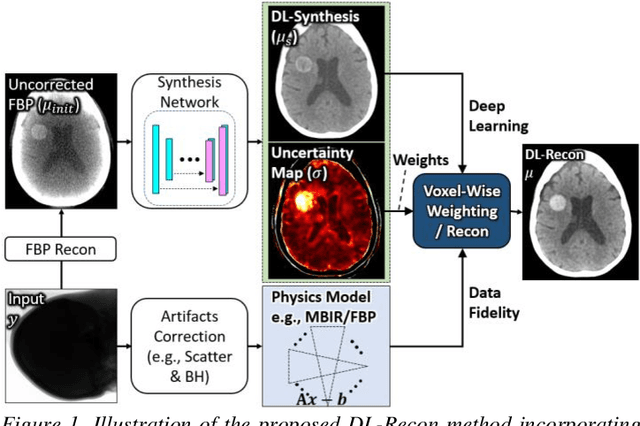
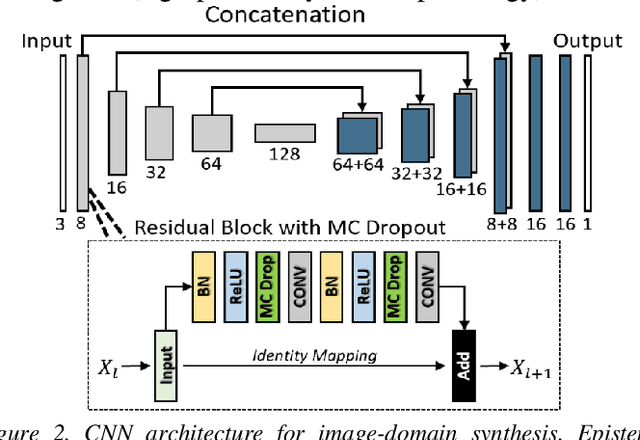
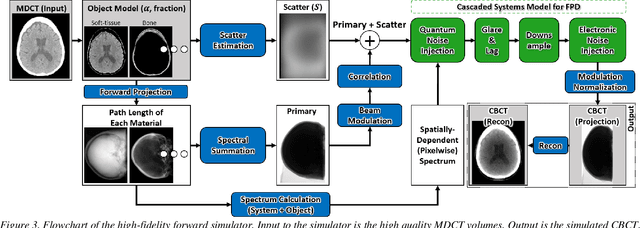
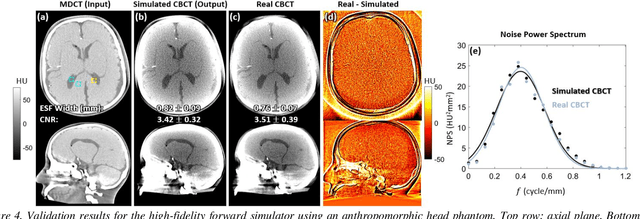
Contrast resolution beyond the limits of conventional cone-beam CT (CBCT) systems is essential to high-quality imaging of the brain. We present a deep learning reconstruction method (dubbed DL-Recon) that integrates physically principled reconstruction models with DL-based image synthesis based on the statistical uncertainty in the synthesis image. A synthesis network was developed to generate a synthesized CBCT image (DL-Synthesis) from an uncorrected filtered back-projection (FBP) image. To improve generalizability (including accurate representation of lesions not seen in training), voxel-wise epistemic uncertainty of DL-Synthesis was computed using a Bayesian inference technique (Monte-Carlo dropout). In regions of high uncertainty, the DL-Recon method incorporates information from a physics-based reconstruction model and artifact-corrected projection data. Two forms of the DL-Recon method are proposed: (i) image-domain fusion of DL-Synthesis and FBP (DL-FBP) weighted by DL uncertainty; and (ii) a model-based iterative image reconstruction (MBIR) optimization using DL-Synthesis to compute a spatially varying regularization term based on DL uncertainty (DL-MBIR). The error in DL-Synthesis images was correlated with the uncertainty in the synthesis estimate. Compared to FBP and PWLS, the DL-Recon methods (both DL-FBP and DL-MBIR) showed ~50% reduction in noise (at matched spatial resolution) and ~40-70% improvement in image uniformity. Conventional DL-Synthesis alone exhibited ~10-60% under-estimation of lesion contrast and ~5-40% reduction in lesion segmentation accuracy (Dice coefficient) in simulated and real brain lesions, suggesting a lack of reliability / generalizability for structures unseen in the training data. DL-FBP and DL-MBIR improved the accuracy of reconstruction by directly incorporating information from the measurements in regions of high uncertainty.

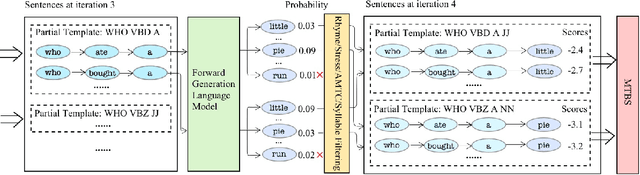
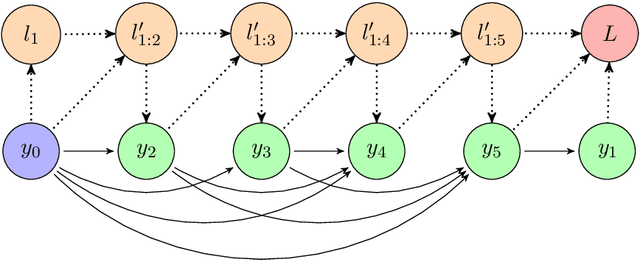
There Once Was a Really Bad Poet, It Was Automated but You Didn't Know It

Limerick generation exemplifies some of the most difficult challenges faced in poetry generation, as the poems must tell a story in only five lines, with constraints on rhyme, stress, and meter. To address these challenges, we introduce LimGen, a novel and fully automated system for limerick generation that outperforms state-of-the-art neural network-based poetry models, as well as prior rule-based poetry models. LimGen consists of three important pieces: the Adaptive Multi-Templated Constraint algorithm that constrains our search to the space of realistic poems, the Multi-Templated Beam Search algorithm which searches efficiently through the space, and the probabilistic Storyline algorithm that provides coherent storylines related to a user-provided prompt word. The resulting limericks satisfy poetic constraints and have thematically coherent storylines, which are sometimes even funny (when we are lucky).

Bayesian neural networks for weak solution of PDEs with uncertainty quantification

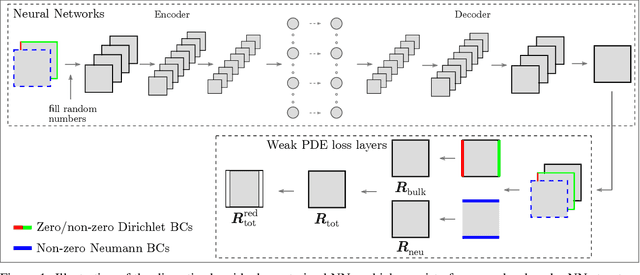
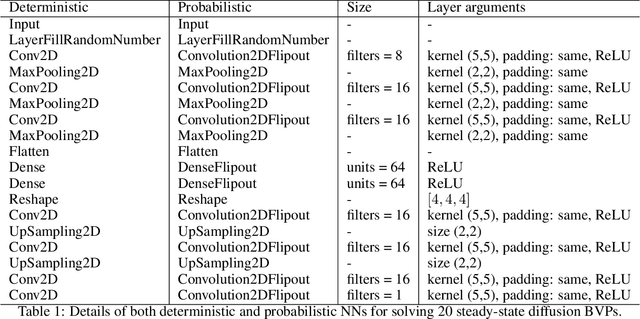
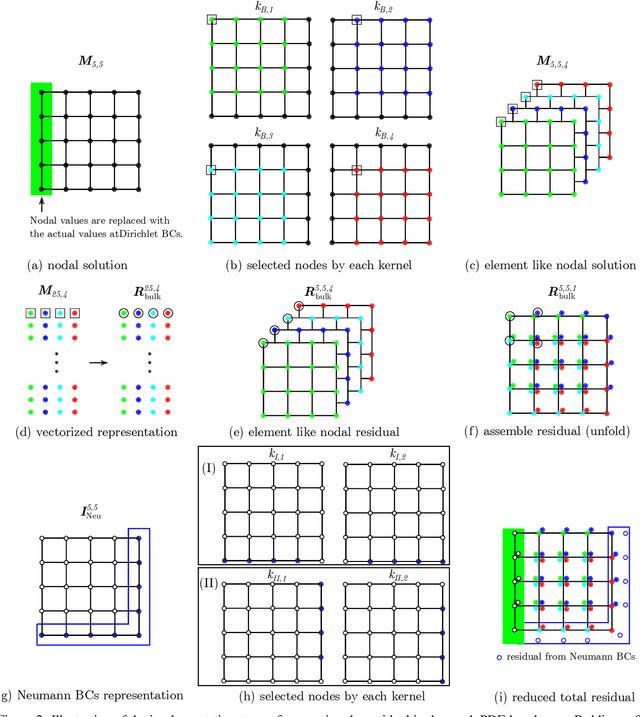
Solving partial differential equations (PDEs) is the canonical approach for understanding the behavior of physical systems. However, large scale solutions of PDEs using state of the art discretization techniques remains an expensive proposition. In this work, a new physics-constrained neural network (NN) approach is proposed to solve PDEs without labels, with a view to enabling high-throughput solutions in support of design and decision-making. Distinct from existing physics-informed NN approaches, where the strong form or weak form of PDEs are used to construct the loss function, we write the loss function of NNs based on the discretized residual of PDEs through an efficient, convolutional operator-based, and vectorized implementation. We explore an encoder-decoder NN structure for both deterministic and probabilistic models, with Bayesian NNs (BNNs) for the latter, which allow us to quantify both epistemic uncertainty from model parameters and aleatoric uncertainty from noise in the data. For BNNs, the discretized residual is used to construct the likelihood function. In our approach, both deterministic and probabilistic convolutional layers are used to learn the applied boundary conditions (BCs) and to detect the problem domain. As both Dirichlet and Neumann BCs are specified as inputs to NNs, a single NN can solve for similar physics, but with different BCs and on a number of problem domains. The trained surrogate PDE solvers can also make interpolating and extrapolating (to a certain extent) predictions for BCs that they were not exposed to during training. Such surrogate models are of particular importance for problems, where similar types of PDEs need to be repeatedly solved for many times with slight variations. We demonstrate the capability and performance of the proposed framework by applying it to steady-state diffusion, linear elasticity, and nonlinear elasticity.

Fast Rates of ERM and Stochastic Approximation: Adaptive to Error Bound Conditions

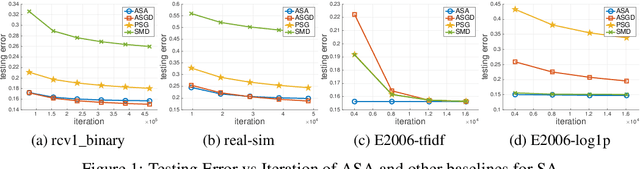
Error bound conditions (EBC) are properties that characterize the growth of an objective function when a point is moved away from the optimal set. They have recently received increasing attention in the field of optimization for developing optimization algorithms with fast convergence. However, the studies of EBC in statistical learning are hitherto still limited. The main contributions of this paper are two-fold. First, we develop fast and intermediate rates of empirical risk minimization (ERM) under EBC for risk minimization with Lipschitz continuous, and smooth convex random functions. Second, we establish fast and intermediate rates of an efficient stochastic approximation (SA) algorithm for risk minimization with Lipschitz continuous random functions, which requires only one pass of $n$ samples and adapts to EBC. For both approaches, the convergence rates span a full spectrum between $\widetilde O(1/\sqrt{n})$ and $\widetilde O(1/n)$ depending on the power constant in EBC, and could be even faster than $O(1/n)$ in special cases for ERM. Moreover, these convergence rates are automatically adaptive without using any knowledge of EBC. Overall, this work not only strengthens the understanding of ERM for statistical learning but also brings new fast stochastic algorithms for solving a broad range of statistical learning problems.