Accurate Data-Driven Surrogates of Dynamical Systems for Forward Propagation of Uncertainty

Stochastic collocation (SC) is a well-known non-intrusive method of constructing surrogate models for uncertainty quantification. In dynamical systems, SC is especially suited for full-field uncertainty propagation that characterizes the distributions of the high-dimensional primary solution fields of a model with stochastic input parameters. However, due to the highly nonlinear nature of the parameter-to-solution map in even the simplest dynamical systems, the constructed SC surrogates are often inaccurate. This work presents an alternative approach, where we apply the SC approximation over the dynamics of the model, rather than the solution. By combining the data-driven sparse identification of nonlinear dynamics (SINDy) framework with SC, we construct dynamics surrogates and integrate them through time to construct the surrogate solutions. We demonstrate that the SC-over-dynamics framework leads to smaller errors, both in terms of the approximated system trajectories as well as the model state distributions, when compared against full-field SC applied to the solutions directly. We present numerical evidence of this improvement using three test problems: a chaotic ordinary differential equation, and two partial differential equations from solid mechanics.

Continuous-variable neural-network quantum states and the quantum rotor model

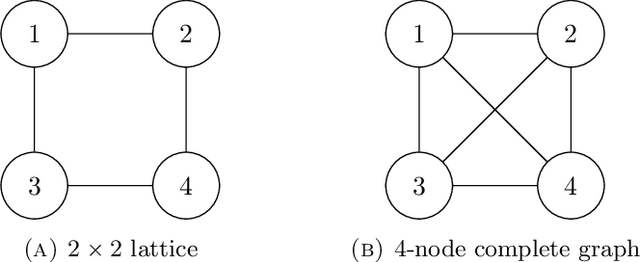
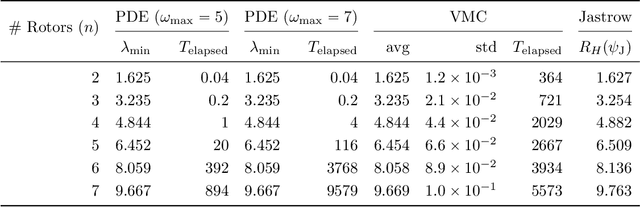
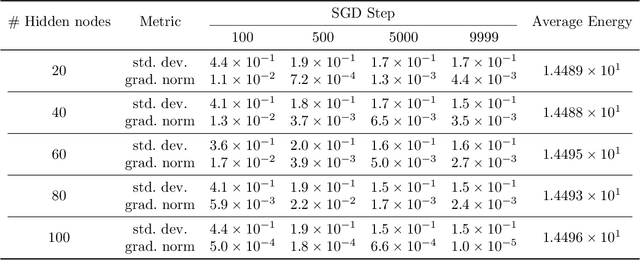
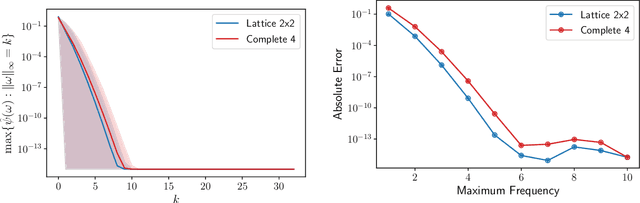
We initiate the study of neural-network quantum state algorithms for analyzing continuous-variable lattice quantum systems in first quantization. A simple family of continuous-variable trial wavefunctons is introduced which naturally generalizes the restricted Boltzmann machine (RBM) wavefunction introduced for analyzing quantum spin systems. By virtue of its simplicity, the same variational Monte Carlo training algorithms that have been developed for ground state determination and time evolution of spin systems have natural analogues in the continuum. We offer a proof of principle demonstration in the context of ground state determination of a stoquastic quantum rotor Hamiltonian. Results are compared against those obtained from partial differential equation (PDE) based scalable eigensolvers. This study serves as a benchmark against which future investigation of continuous-variable neural quantum states can be compared, and points to the need to consider deep network architectures and more sophisticated training algorithms.

Efficient MCMC Sampling for Bayesian Matrix Factorization by Breaking Posterior Symmetries

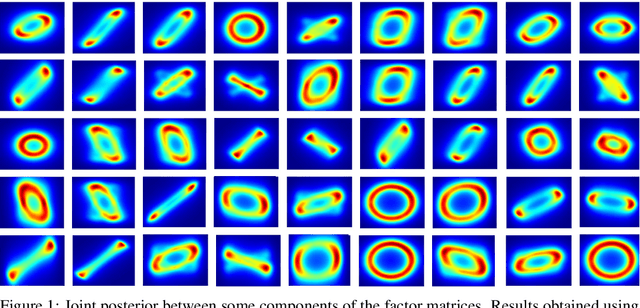
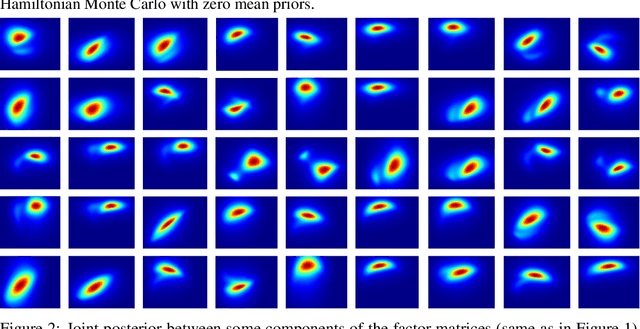
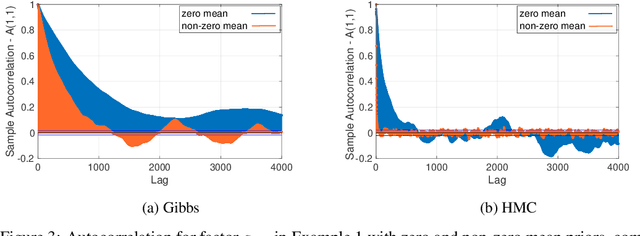
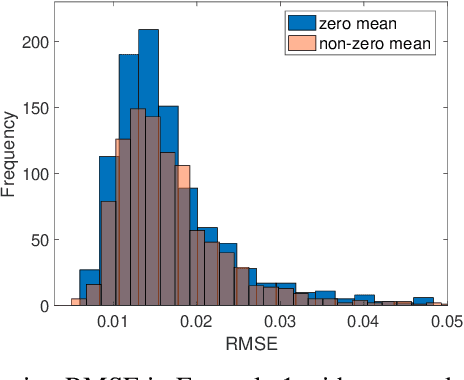
Bayesian low-rank matrix factorization techniques have become an essential tool for relational data analysis and matrix completion. A standard approach is to assign zero-mean Gaussian priors on the columns or rows of factor matrices to create a conjugate system. This choice of prior leads to symmetries in the posterior distribution and can severely reduce the efficiency of Markov-chain Monte-Carlo (MCMC) sampling approaches. In this paper, we propose a simple modification to the prior choice that provably breaks these symmetries and maintains/improves accuracy. Specifically, we provide conditions that the Gaussian prior mean and covariance must satisfy so the posterior does not exhibit invariances that yield sampling difficulties. For example, we show that using non-zero linearly independent prior means significantly lowers the autocorrelation of MCMC samples, and can also lead to lower reconstruction errors.