Variational quantum and neural quantum states algorithms for the linear complementarity problem

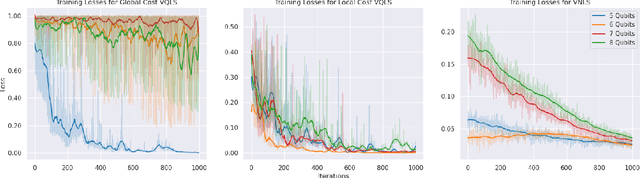
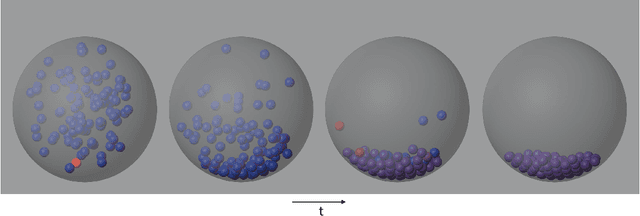
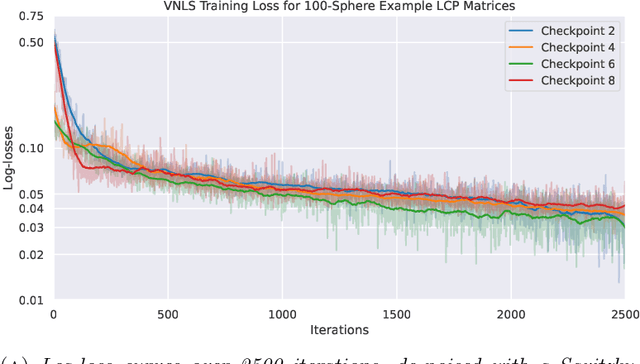
Variational quantum algorithms (VQAs) are promising hybrid quantum-classical methods designed to leverage the computational advantages of quantum computing while mitigating the limitations of current noisy intermediate-scale quantum (NISQ) hardware. Although VQAs have been demonstrated as proofs of concept, their practical utility in solving real-world problems -- and whether quantum-inspired classical algorithms can match their performance -- remains an open question. We present a novel application of the variational quantum linear solver (VQLS) and its classical neural quantum states-based counterpart, the variational neural linear solver (VNLS), as key components within a minimum map Newton solver for a complementarity-based rigid body contact model. We demonstrate using the VNLS that our solver accurately simulates the dynamics of rigid spherical bodies during collision events. These results suggest that quantum and quantum-inspired linear algebra algorithms can serve as viable alternatives to standard linear algebra solvers for modeling certain physical systems.