Efficient MCMC Sampling for Bayesian Matrix Factorization by Breaking Posterior Symmetries

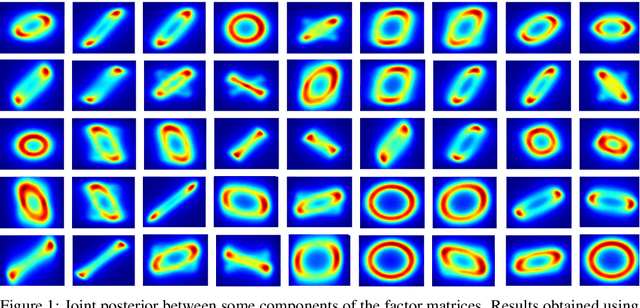
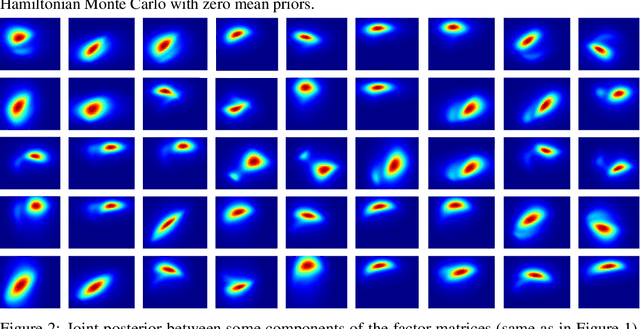
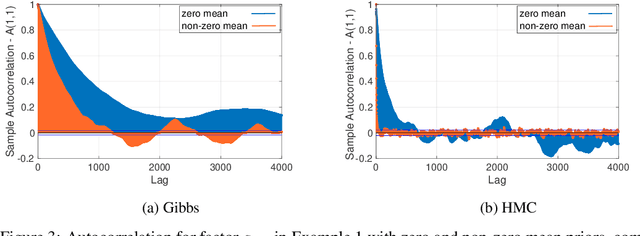
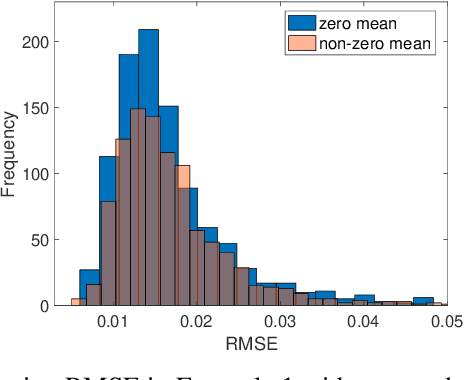
Bayesian low-rank matrix factorization techniques have become an essential tool for relational data analysis and matrix completion. A standard approach is to assign zero-mean Gaussian priors on the columns or rows of factor matrices to create a conjugate system. This choice of prior leads to symmetries in the posterior distribution and can severely reduce the efficiency of Markov-chain Monte-Carlo (MCMC) sampling approaches. In this paper, we propose a simple modification to the prior choice that provably breaks these symmetries and maintains/improves accuracy. Specifically, we provide conditions that the Gaussian prior mean and covariance must satisfy so the posterior does not exhibit invariances that yield sampling difficulties. For example, we show that using non-zero linearly independent prior means significantly lowers the autocorrelation of MCMC samples, and can also lead to lower reconstruction errors.