Can KAN CANs? Input-convex Kolmogorov-Arnold Networks (KANs) as hyperelastic constitutive artificial neural networks (CANs)

Traditional constitutive models rely on hand-crafted parametric forms with limited expressivity and generalizability, while neural network-based models can capture complex material behavior but often lack interpretability. To balance these trade-offs, we present Input-Convex Kolmogorov-Arnold Networks (ICKANs) for learning polyconvex hyperelastic constitutive laws. ICKANs leverage the Kolmogorov-Arnold representation, decomposing the model into compositions of trainable univariate spline-based activation functions for rich expressivity. We introduce trainable input-convex splines within the KAN architecture, ensuring physically admissible polyconvex hyperelastic models. The resulting models are both compact and interpretable, enabling explicit extraction of analytical constitutive relationships through an input-convex symbolic regression techinque. Through unsupervised training on full-field strain data and limited global force measurements, ICKANs accurately capture nonlinear stress-strain behavior across diverse strain states. Finite element simulations of unseen geometries with trained ICKAN hyperelastic constitutive models confirm the framework's robustness and generalization capability.

Inverse Design of Vitrimeric Polymers by Molecular Dynamics and Generative Modeling

Vitrimer is a new class of sustainable polymers with the ability of self-healing through rearrangement of dynamic covalent adaptive networks. However, a limited choice of constituent molecules restricts their property space, prohibiting full realization of their potential applications. Through a combination of molecular dynamics (MD) simulations and machine learning (ML), particularly a novel graph variational autoencoder (VAE) model, we establish a method for generating novel vitrimers and guide their inverse design based on desired glass transition temperature (Tg). We build the first vitrimer dataset of one million and calculate Tg on 8,424 of them by high-throughput MD simulations calibrated by a Gaussian process model. The proposed VAE employs dual graph encoders and a latent dimension overlapping scheme which allows for individual representation of multi-component vitrimers. By constructing a continuous latent space containing necessary information of vitrimers, we demonstrate high accuracy and efficiency of our framework in discovering novel vitrimers with desirable Tg beyond the training regime. The proposed vitrimers with reasonable synthesizability cover a wide range of Tg and broaden the potential widespread usage of vitrimeric materials.

NN-EUCLID: deep-learning hyperelasticity without stress data

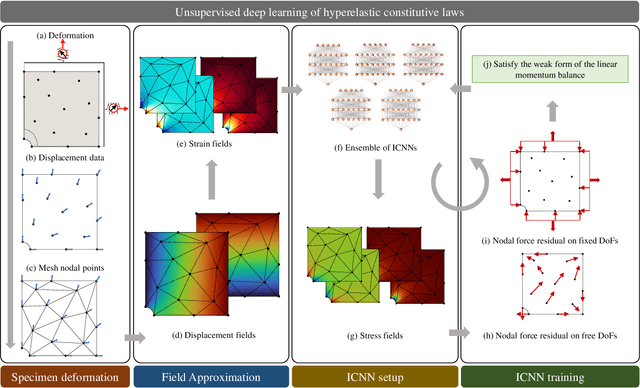
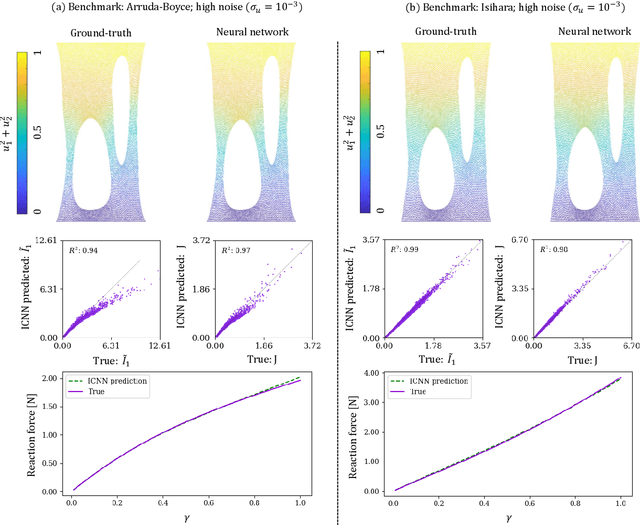
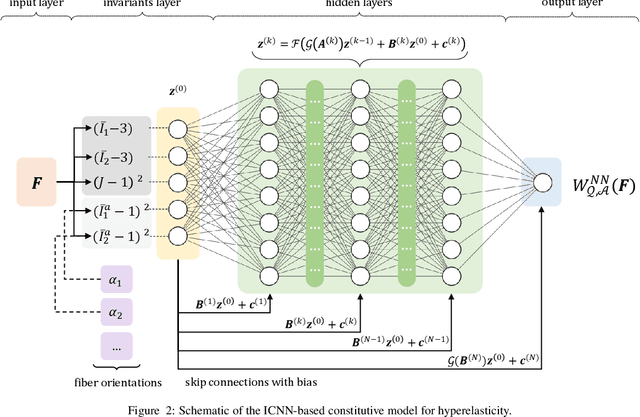
We propose a new approach for unsupervised learning of hyperelastic constitutive laws with physics-consistent deep neural networks. In contrast to supervised learning, which assumes the availability of stress-strain pairs, the approach only uses realistically measurable full-field displacement and global reaction force data, thus it lies within the scope of our recent framework for Efficient Unsupervised Constitutive Law Identification and Discovery (EUCLID) and we denote it as NN-EUCLID. The absence of stress labels is compensated for by leveraging a physics-motivated loss function based on the conservation of linear momentum to guide the learning process. The constitutive model is based on input-convex neural networks, which are capable of learning a function that is convex with respect to its inputs. By employing a specially designed neural network architecture, multiple physical and thermodynamic constraints for hyperelastic constitutive laws, such as material frame indifference, (poly-)convexity, and stress-free reference configuration are automatically satisfied. We demonstrate the ability of the approach to accurately learn several hidden isotropic and anisotropic hyperelastic constitutive laws - including e.g., Mooney-Rivlin, Arruda-Boyce, Ogden, and Holzapfel models - without using stress data. For anisotropic hyperelasticity, the unknown anisotropic fiber directions are automatically discovered jointly with the constitutive model. The neural network-based constitutive models show good generalization capability beyond the strain states observed during training and are readily deployable in a general finite element framework for simulating complex mechanical boundary value problems with good accuracy.