NN-EUCLID: deep-learning hyperelasticity without stress data
Paper and Code
May 04, 2022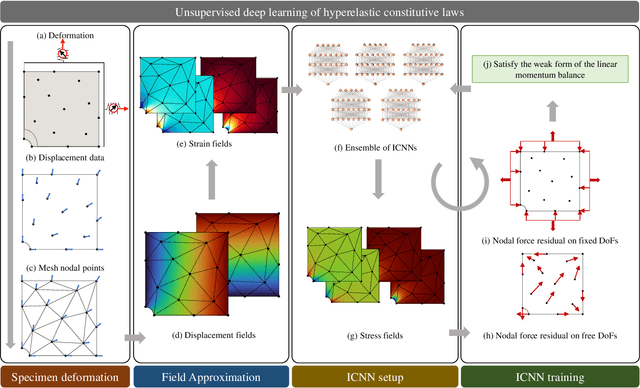
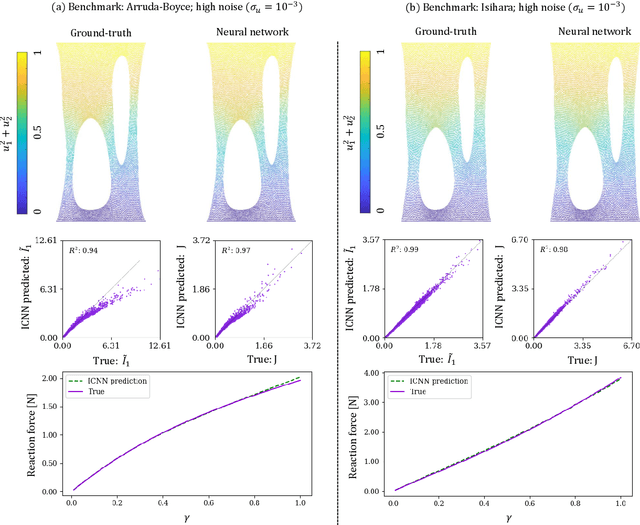

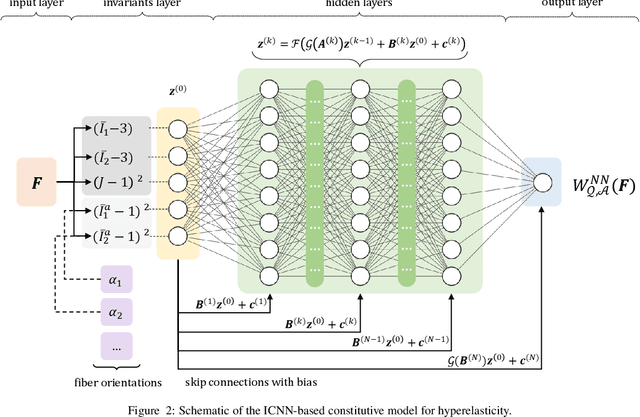
We propose a new approach for unsupervised learning of hyperelastic constitutive laws with physics-consistent deep neural networks. In contrast to supervised learning, which assumes the availability of stress-strain pairs, the approach only uses realistically measurable full-field displacement and global reaction force data, thus it lies within the scope of our recent framework for Efficient Unsupervised Constitutive Law Identification and Discovery (EUCLID) and we denote it as NN-EUCLID. The absence of stress labels is compensated for by leveraging a physics-motivated loss function based on the conservation of linear momentum to guide the learning process. The constitutive model is based on input-convex neural networks, which are capable of learning a function that is convex with respect to its inputs. By employing a specially designed neural network architecture, multiple physical and thermodynamic constraints for hyperelastic constitutive laws, such as material frame indifference, (poly-)convexity, and stress-free reference configuration are automatically satisfied. We demonstrate the ability of the approach to accurately learn several hidden isotropic and anisotropic hyperelastic constitutive laws - including e.g., Mooney-Rivlin, Arruda-Boyce, Ogden, and Holzapfel models - without using stress data. For anisotropic hyperelasticity, the unknown anisotropic fiber directions are automatically discovered jointly with the constitutive model. The neural network-based constitutive models show good generalization capability beyond the strain states observed during training and are readily deployable in a general finite element framework for simulating complex mechanical boundary value problems with good accuracy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge