Mike Michelis
Vandermonde Neural Operators
Jun 05, 2023Abstract:Fourier Neural Operators (FNOs) have emerged as very popular machine learning architectures for learning operators, particularly those arising in PDEs. However, as FNOs rely on the fast Fourier transform for computational efficiency, the architecture can be limited to input data on equispaced Cartesian grids. Here, we generalize FNOs to handle input data on non-equispaced point distributions. Our proposed model, termed as Vandermonde Neural Operator (VNO), utilizes Vandermonde-structured matrices to efficiently compute forward and inverse Fourier transforms, even on arbitrarily distributed points. We present numerical experiments to demonstrate that VNOs can be significantly faster than FNOs, while retaining comparable accuracy, and improve upon accuracy of comparable non-equispaced methods such as the Geo-FNO.
Sim-to-Real for Soft Robots using Differentiable FEM: Recipes for Meshing, Damping, and Actuation
Feb 17, 2022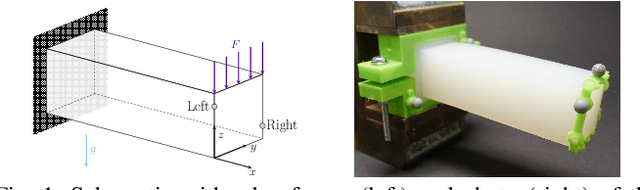
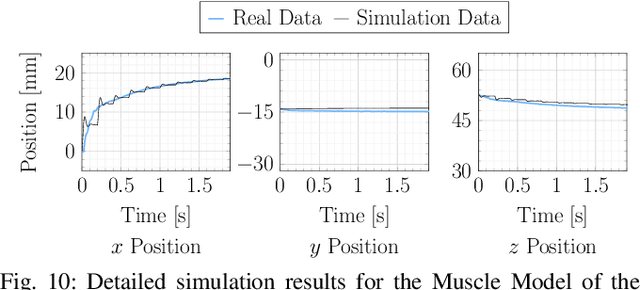
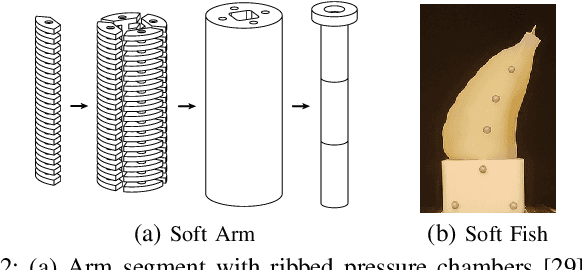
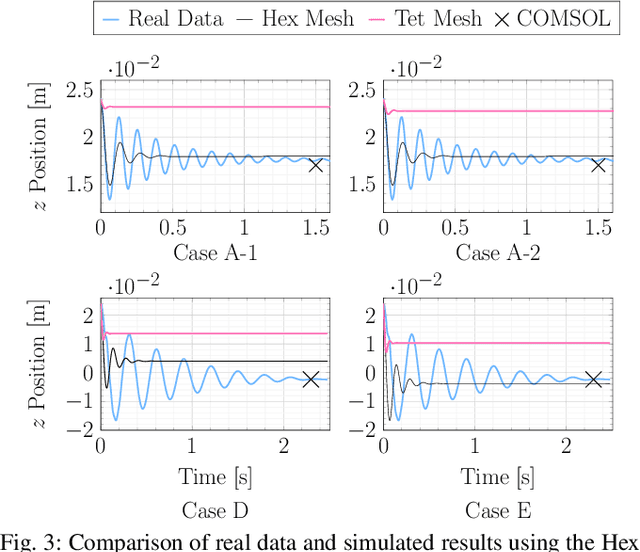
Abstract:An accurate, physically-based, and differentiable model of soft robots can unlock downstream applications in optimal control. The Finite Element Method (FEM) is an expressive approach for modeling highly deformable structures such as dynamic, elastomeric soft robots. In this paper, we compare virtual robot models simulated using differentiable FEM with measurements from their physical counterparts. In particular, we examine several soft structures with different morphologies: a clamped soft beam under external force, a pneumatically actuated soft robotic arm, and a soft robotic fish tail. We benchmark and analyze different meshing resolutions and elements (tetrahedra and hexahedra), numerical damping, and the efficacy of differentiability for parameter calibration using a simulator based on the fast Differentiable Projective Dynamics (DiffPD). We also advance FEM modeling in application to soft robotics by proposing a predictive model for pneumatic soft robotic actuation. Through our recipes and case studies, we provide strategies and algorithms for matching real-world physics in simulation, making FEM useful for soft robots
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge