Learning a Gaussian Mixture for Sparsity Regularization in Inverse Problems

In inverse problems, it is widely recognized that the incorporation of a sparsity prior yields a regularization effect on the solution. This approach is grounded on the a priori assumption that the unknown can be appropriately represented in a basis with a limited number of significant components, while most coefficients are close to zero. This occurrence is frequently observed in real-world scenarios, such as with piecewise smooth signals. In this study, we propose a probabilistic sparsity prior formulated as a mixture of degenerate Gaussians, capable of modeling sparsity with respect to a generic basis. Under this premise, we design a neural network that can be interpreted as the Bayes estimator for linear inverse problems. Additionally, we put forth both a supervised and an unsupervised training strategy to estimate the parameters of this network. To evaluate the effectiveness of our approach, we conduct a numerical comparison with commonly employed sparsity-promoting regularization techniques, namely LASSO, group LASSO, iterative hard thresholding, and sparse coding/dictionary learning. Notably, our reconstructions consistently exhibit lower mean square error values across all $1$D datasets utilized for the comparisons, even in cases where the datasets significantly deviate from a Gaussian mixture model.

Learned reconstruction methods for inverse problems: sample error estimates

Learning-based and data-driven techniques have recently become a subject of primary interest in the field of reconstruction and regularization of inverse problems. Besides the development of novel methods, yielding excellent results in several applications, their theoretical investigation has attracted growing interest, e.g., on the topics of reliability, stability, and interpretability. In this work, a general framework is described, allowing us to interpret many of these techniques in the context of statistical learning. This is not intended to provide a complete survey of existing methods, but rather to put them in a working perspective, which naturally allows their theoretical treatment. The main goal of this dissertation is thereby to address the generalization properties of learned reconstruction methods, and specifically to perform their sample error analysis. This task, well-developed in statistical learning, consists in estimating the dependence of the learned operators with respect to the data employed for their training. A rather general strategy is proposed, whose assumptions are met for a large class of inverse problems and learned methods, as depicted via a selection of examples.

Learning the optimal regularizer for inverse problems

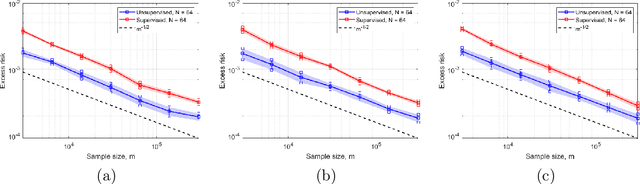
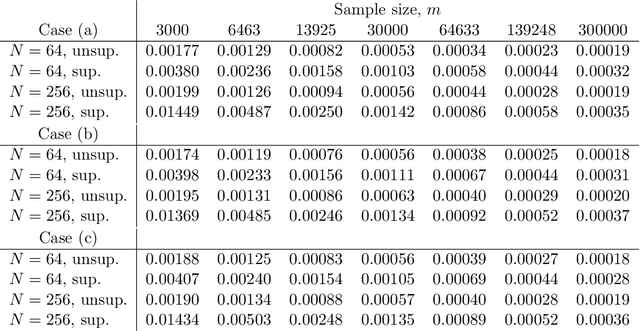
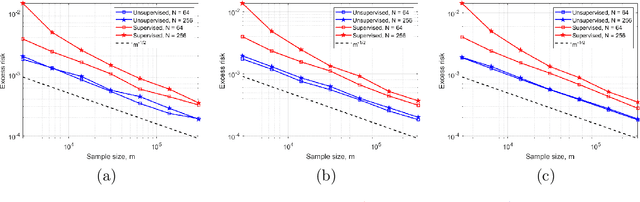
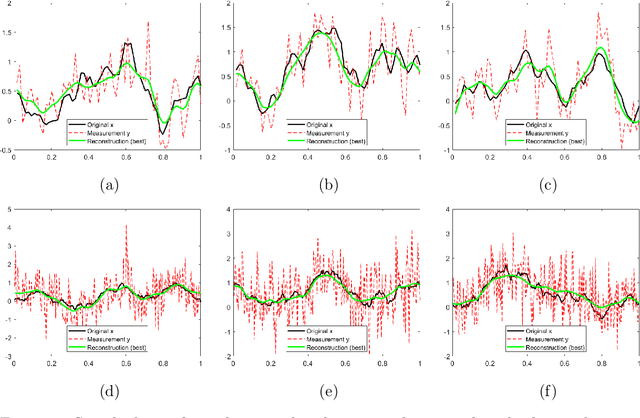
In this work, we consider the linear inverse problem $y=Ax+\epsilon$, where $A\colon X\to Y$ is a known linear operator between the separable Hilbert spaces $X$ and $Y$, $x$ is a random variable in $X$ and $\epsilon$ is a zero-mean random process in $Y$. This setting covers several inverse problems in imaging including denoising, deblurring, and X-ray tomography. Within the classical framework of regularization, we focus on the case where the regularization functional is not given a priori but learned from data. Our first result is a characterization of the optimal generalized Tikhonov regularizer, with respect to the mean squared error. We find that it is completely independent of the forward operator $A$ and depends only on the mean and covariance of $x$. Then, we consider the problem of learning the regularizer from a finite training set in two different frameworks: one supervised, based on samples of both $x$ and $y$, and one unsupervised, based only on samples of $x$. In both cases, we prove generalization bounds, under some weak assumptions on the distribution of $x$ and $\epsilon$, including the case of sub-Gaussian variables. Our bounds hold in infinite-dimensional spaces, thereby showing that finer and finer discretizations do not make this learning problem harder. The results are validated through numerical simulations.

Convex regularization in statistical inverse learning problems

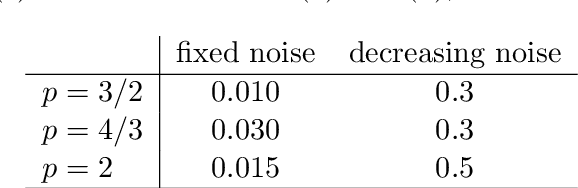
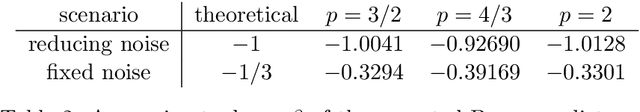
We consider a statistical inverse learning problem, where the task is to estimate a function $f$ based on noisy point evaluations of $Af$, where $A$ is a linear operator. The function $Af$ is evaluated at i.i.d. random design points $u_n$, $n=1,...,N$ generated by an unknown general probability distribution. We consider Tikhonov regularization with general convex and $p$-homogeneous penalty functionals and derive concentration rates of the regularized solution to the ground truth measured in the symmetric Bregman distance induced by the penalty functional. We derive concrete rates for Besov norm penalties and numerically demonstrate the correspondence with the observed rates in the context of X-ray tomography.

Deep neural networks for inverse problems with pseudodifferential operators: an application to limited-angle tomography

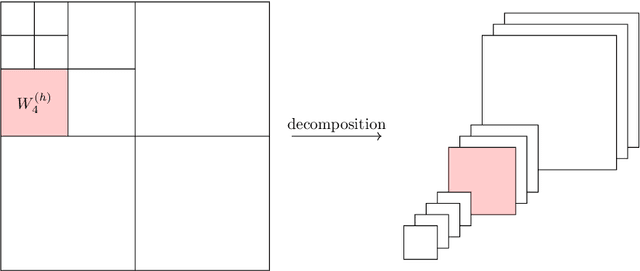
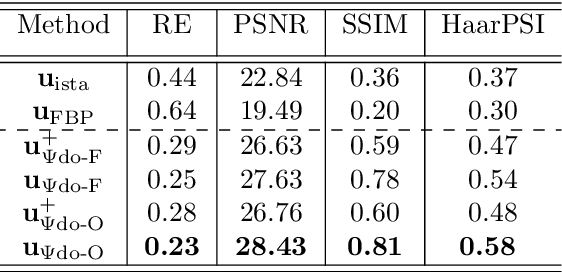
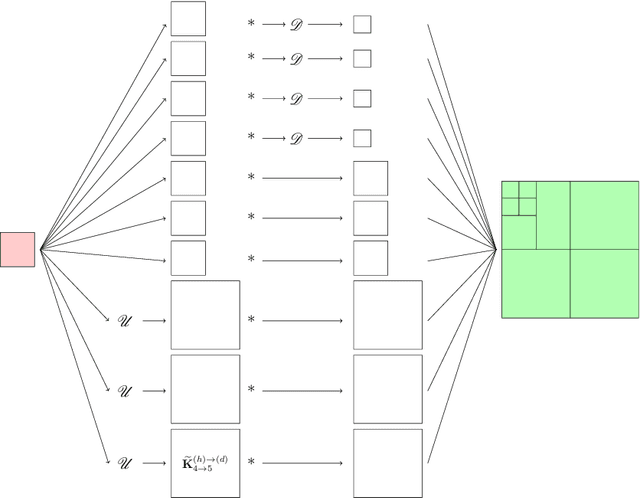
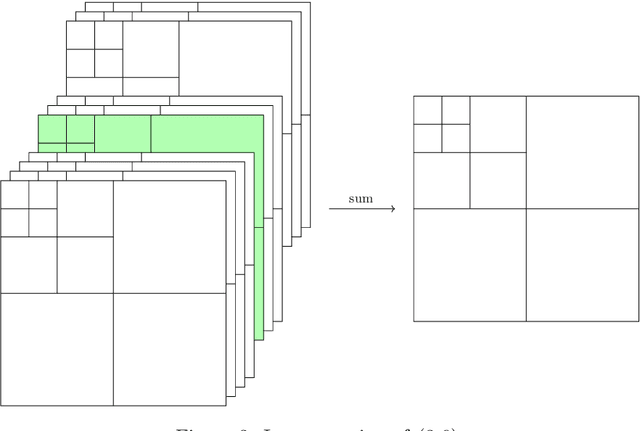
We propose a novel convolutional neural network (CNN), called $\Psi$DONet, designed for learning pseudodifferential operators ($\Psi$DOs) in the context of linear inverse problems. Our starting point is the Iterative Soft Thresholding Algorithm (ISTA), a well-known algorithm to solve sparsity-promoting minimization problems. We show that, under rather general assumptions on the forward operator, the unfolded iterations of ISTA can be interpreted as the successive layers of a CNN, which in turn provides fairly general network architectures that, for a specific choice of the parameters involved, allow to reproduce ISTA, or a perturbation of ISTA for which we can bound the coefficients of the filters. Our case study is the limited-angle X-ray transform and its application to limited-angle computed tomography (LA-CT). In particular, we prove that, in the case of LA-CT, the operations of upscaling, downscaling and convolution, which characterize our $\Psi$DONet and most deep learning schemes, can be exactly determined by combining the convolutional nature of the limited angle X-ray transform and basic properties defining an orthogonal wavelet system. We test two different implementations of $\Psi$DONet on simulated data from limited-angle geometry, generated from the ellipse data set. Both implementations provide equally good and noteworthy preliminary results, showing the potential of the approach we propose and paving the way to applying the same idea to other convolutional operators which are $\Psi$DOs or Fourier integral operators.