Explainable bilevel optimization: an application to the Helsinki deblur challenge

In this paper we present a bilevel optimization scheme for the solution of a general image deblurring problem, in which a parametric variational-like approach is encapsulated within a machine learning scheme to provide a high quality reconstructed image with automatically learned parameters. The ingredients of the variational lower level and the machine learning upper one are specifically chosen for the Helsinki Deblur Challenge 2021, in which sequences of letters are asked to be recovered from out-of-focus photographs with increasing levels of blur. Our proposed procedure for the reconstructed image consists in a fixed number of FISTA iterations applied to the minimization of an edge preserving and binarization enforcing regularized least-squares functional. The parameters defining the variational model and the optimization steps, which, unlike most deep learning approaches, all have a precise and interpretable meaning, are learned via either a similarity index or a support vector machine strategy. Numerical experiments on the test images provided by the challenge authors show significant gains with respect to a standard variational approach and performances comparable with those of some of the proposed deep learning based algorithms which require the optimization of millions of parameters.

DCT-Former: Efficient Self-Attention with Discrete Cosine Transform

Since their introduction the Trasformer architectures emerged as the dominating architectures for both natural language processing and, more recently, computer vision applications. An intrinsic limitation of this family of "fully-attentive" architectures arises from the computation of the dot-product attention, which grows both in memory consumption and number of operations as $O(n^2)$ where $n$ stands for the input sequence length, thus limiting the applications that require modeling very long sequences. Several approaches have been proposed so far in the literature to mitigate this issue, with varying degrees of success. Our idea takes inspiration from the world of lossy data compression (such as the JPEG algorithm) to derive an approximation of the attention module by leveraging the properties of the Discrete Cosine Transform. An extensive section of experiments shows that our method takes up less memory for the same performance, while also drastically reducing inference time. This makes it particularly suitable in real-time contexts on embedded platforms. Moreover, we assume that the results of our research might serve as a starting point for a broader family of deep neural models with reduced memory footprint. The implementation will be made publicly available at https://github.com/cscribano/DCT-Former-Public

Deep neural networks for inverse problems with pseudodifferential operators: an application to limited-angle tomography

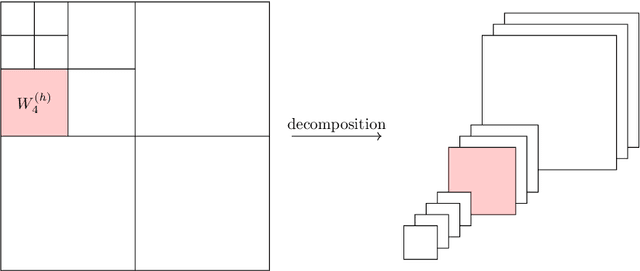
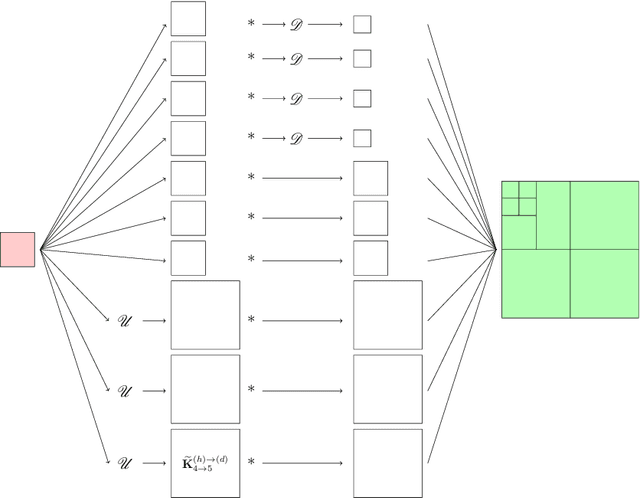
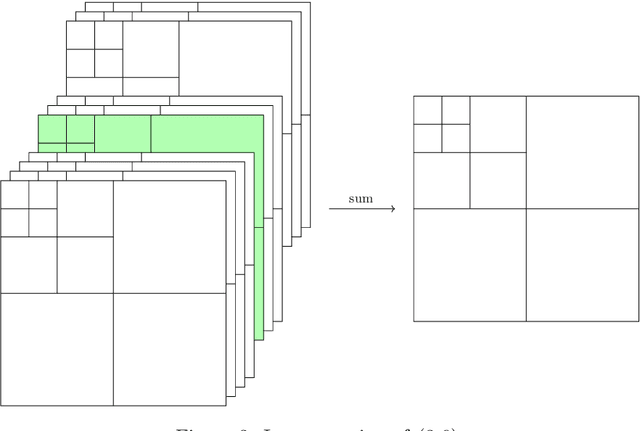
We propose a novel convolutional neural network (CNN), called $\Psi$DONet, designed for learning pseudodifferential operators ($\Psi$DOs) in the context of linear inverse problems. Our starting point is the Iterative Soft Thresholding Algorithm (ISTA), a well-known algorithm to solve sparsity-promoting minimization problems. We show that, under rather general assumptions on the forward operator, the unfolded iterations of ISTA can be interpreted as the successive layers of a CNN, which in turn provides fairly general network architectures that, for a specific choice of the parameters involved, allow to reproduce ISTA, or a perturbation of ISTA for which we can bound the coefficients of the filters. Our case study is the limited-angle X-ray transform and its application to limited-angle computed tomography (LA-CT). In particular, we prove that, in the case of LA-CT, the operations of upscaling, downscaling and convolution, which characterize our $\Psi$DONet and most deep learning schemes, can be exactly determined by combining the convolutional nature of the limited angle X-ray transform and basic properties defining an orthogonal wavelet system. We test two different implementations of $\Psi$DONet on simulated data from limited-angle geometry, generated from the ellipse data set. Both implementations provide equally good and noteworthy preliminary results, showing the potential of the approach we propose and paving the way to applying the same idea to other convolutional operators which are $\Psi$DOs or Fourier integral operators.

A scaled gradient projection method for Bayesian learning in dynamical systems

A crucial task in system identification problems is the selection of the most appropriate model class, and is classically addressed resorting to cross-validation or using asymptotic arguments. As recently suggested in the literature, this can be addressed in a Bayesian framework, where model complexity is regulated by few hyperparameters, which can be estimated via marginal likelihood maximization. It is thus of primary importance to design effective optimization methods to solve the corresponding optimization problem. If the unknown impulse response is modeled as a Gaussian process with a suitable kernel, the maximization of the marginal likelihood leads to a challenging nonconvex optimization problem, which requires a stable and effective solution strategy. In this paper we address this problem by means of a scaled gradient projection algorithm, in which the scaling matrix and the steplength parameter play a crucial role to provide a meaning solution in a computational time comparable with second order methods. In particular, we propose both a generalization of the split gradient approach to design the scaling matrix in the presence of box constraints, and an effective implementation of the gradient and objective function. The extensive numerical experiments carried out on several test problems show that our method is very effective in providing in few tenths of a second solutions of the problems with accuracy comparable with state-of-the-art approaches. Moreover, the flexibility of the proposed strategy makes it easily adaptable to a wider range of problems arising in different areas of machine learning, signal processing and system identification.