4D Dual-Tree Complex Wavelets for Time-Dependent Data

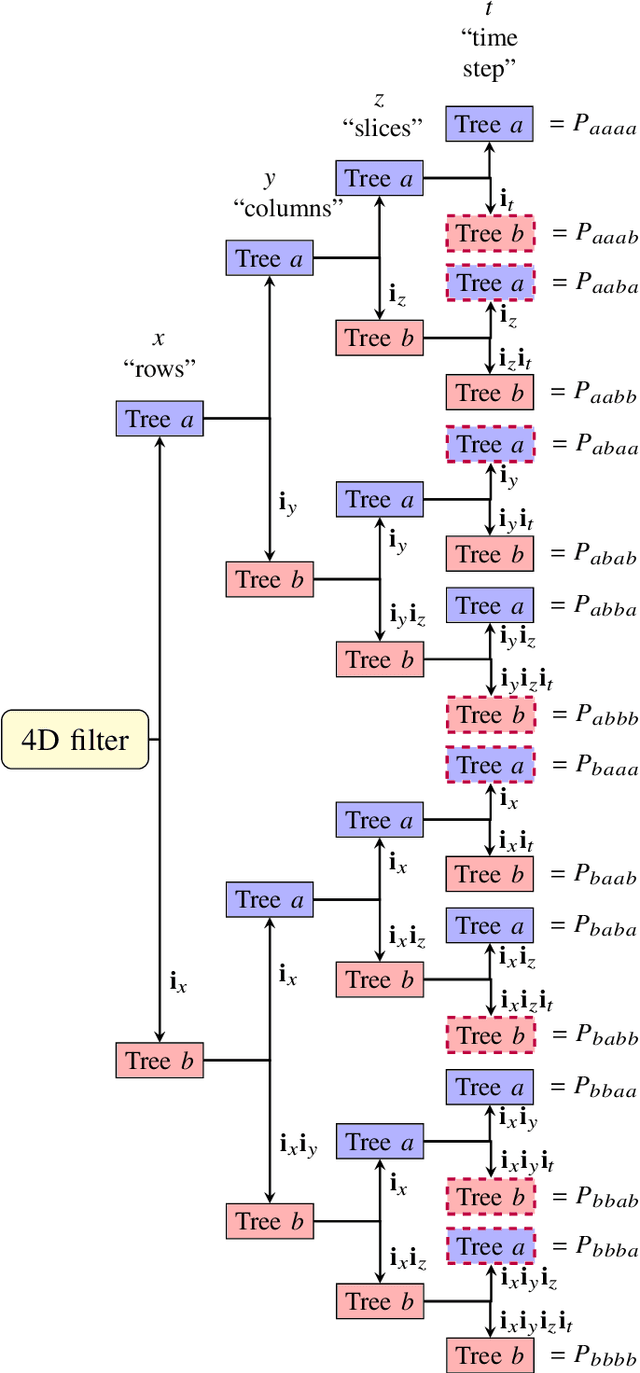
The dual-tree complex wavelet transform (DT-$\mathbb{C}$WT) is extended to the 4D setting. Key properties of 4D DT-$\mathbb{C}$WT, such as directional sensitivity and shift-invariance, are discussed and illustrated in a tomographic application. The inverse problem of reconstructing a dynamic three-dimensional target from X-ray projection measurements can be formulated as 4D space-time tomography. The results suggest that 4D DT-$\mathbb{C}$WT offers simple implementations combined with useful theoretical properties for tomographic reconstruction.

Convex regularization in statistical inverse learning problems

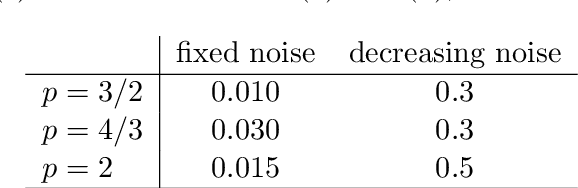
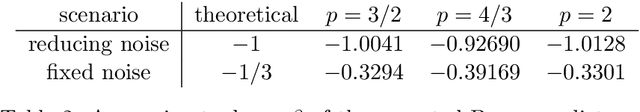
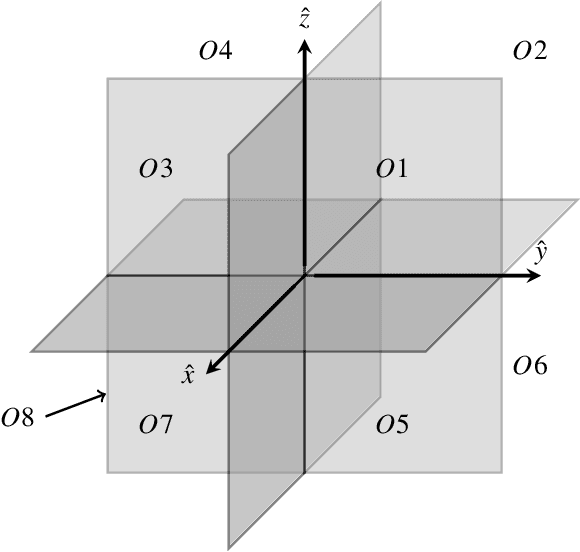
We consider a statistical inverse learning problem, where the task is to estimate a function $f$ based on noisy point evaluations of $Af$, where $A$ is a linear operator. The function $Af$ is evaluated at i.i.d. random design points $u_n$, $n=1,...,N$ generated by an unknown general probability distribution. We consider Tikhonov regularization with general convex and $p$-homogeneous penalty functionals and derive concentration rates of the regularized solution to the ground truth measured in the symmetric Bregman distance induced by the penalty functional. We derive concrete rates for Besov norm penalties and numerically demonstrate the correspondence with the observed rates in the context of X-ray tomography.

Deep neural networks for inverse problems with pseudodifferential operators: an application to limited-angle tomography

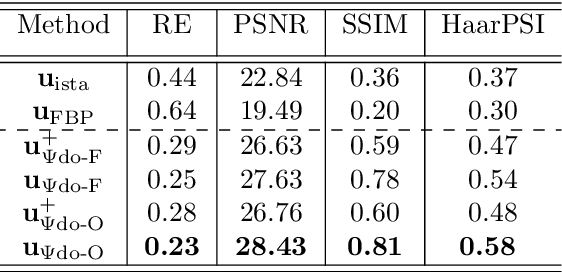
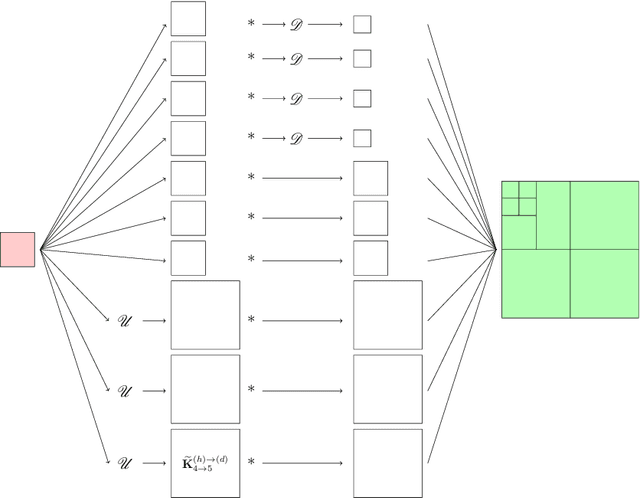
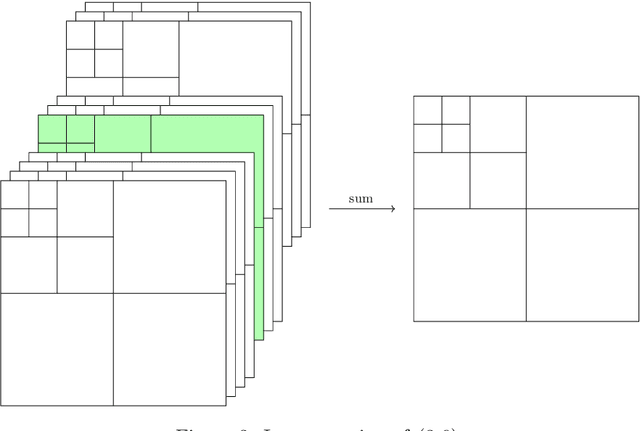
We propose a novel convolutional neural network (CNN), called $\Psi$DONet, designed for learning pseudodifferential operators ($\Psi$DOs) in the context of linear inverse problems. Our starting point is the Iterative Soft Thresholding Algorithm (ISTA), a well-known algorithm to solve sparsity-promoting minimization problems. We show that, under rather general assumptions on the forward operator, the unfolded iterations of ISTA can be interpreted as the successive layers of a CNN, which in turn provides fairly general network architectures that, for a specific choice of the parameters involved, allow to reproduce ISTA, or a perturbation of ISTA for which we can bound the coefficients of the filters. Our case study is the limited-angle X-ray transform and its application to limited-angle computed tomography (LA-CT). In particular, we prove that, in the case of LA-CT, the operations of upscaling, downscaling and convolution, which characterize our $\Psi$DONet and most deep learning schemes, can be exactly determined by combining the convolutional nature of the limited angle X-ray transform and basic properties defining an orthogonal wavelet system. We test two different implementations of $\Psi$DONet on simulated data from limited-angle geometry, generated from the ellipse data set. Both implementations provide equally good and noteworthy preliminary results, showing the potential of the approach we propose and paving the way to applying the same idea to other convolutional operators which are $\Psi$DOs or Fourier integral operators.