4D Dual-Tree Complex Wavelets for Time-Dependent Data

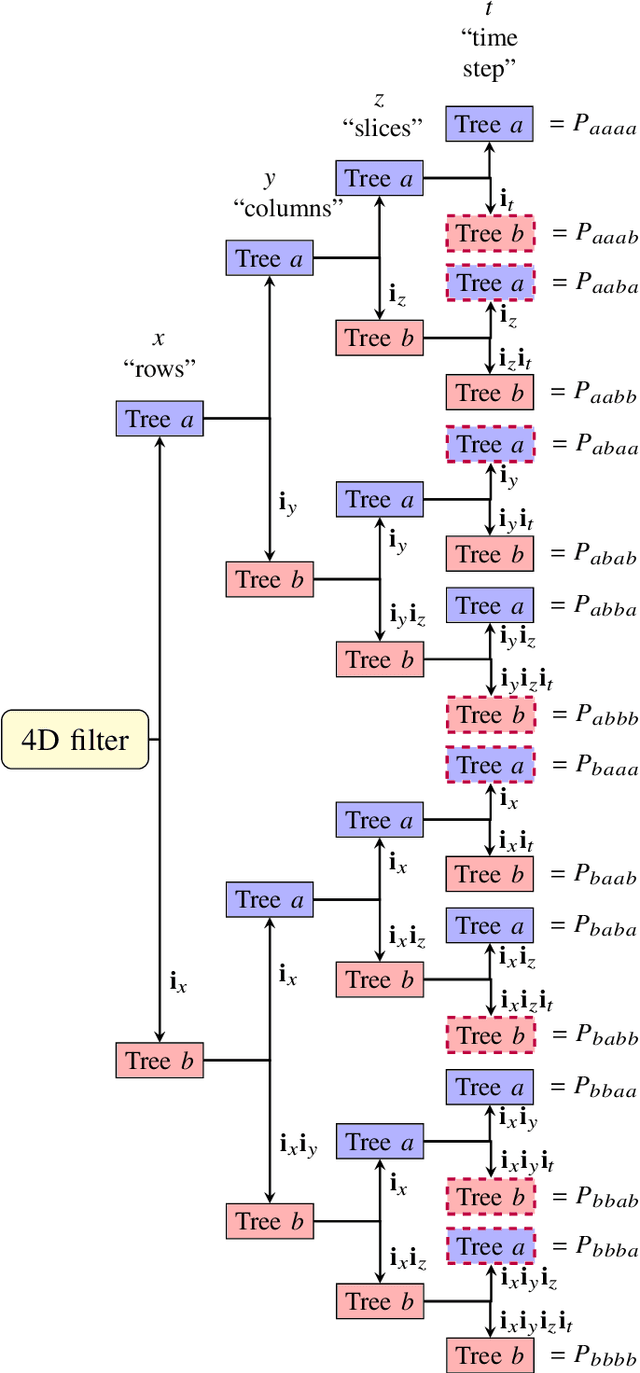
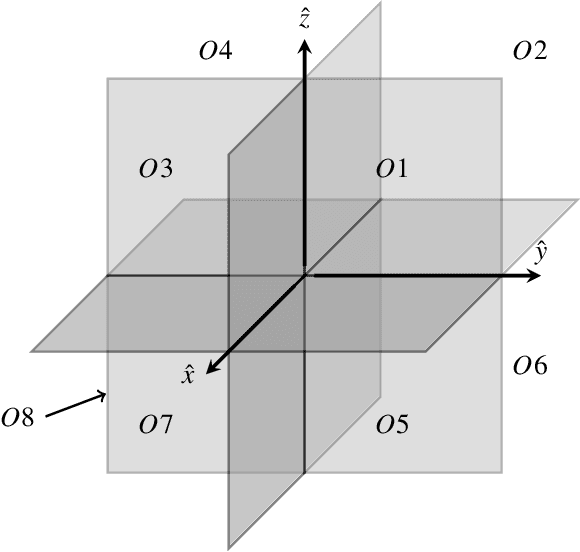
The dual-tree complex wavelet transform (DT-$\mathbb{C}$WT) is extended to the 4D setting. Key properties of 4D DT-$\mathbb{C}$WT, such as directional sensitivity and shift-invariance, are discussed and illustrated in a tomographic application. The inverse problem of reconstructing a dynamic three-dimensional target from X-ray projection measurements can be formulated as 4D space-time tomography. The results suggest that 4D DT-$\mathbb{C}$WT offers simple implementations combined with useful theoretical properties for tomographic reconstruction.