Samuli Siltanen
Learned enclosure method for experimental EIT data
Apr 15, 2025


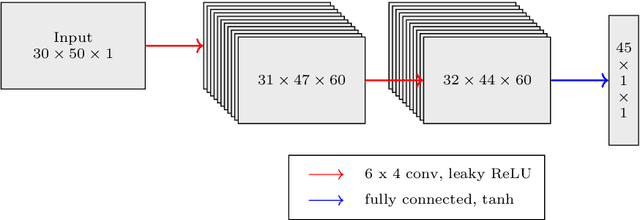
Abstract:Electrical impedance tomography (EIT) is a non-invasive imaging method with diverse applications, including medical imaging and non-destructive testing. The inverse problem of reconstructing internal electrical conductivity from boundary measurements is nonlinear and highly ill-posed, making it difficult to solve accurately. In recent years, there has been growing interest in combining analytical methods with machine learning to solve inverse problems. In this paper, we propose a method for estimating the convex hull of inclusions from boundary measurements by combining the enclosure method proposed by Ikehata with neural networks. We demonstrate its performance using experimental data. Compared to the classical enclosure method with least squares fitting, the learned convex hull achieves superior performance on both simulated and experimental data.
Stroke classification using Virtual Hybrid Edge Detection from in silico electrical impedance tomography data
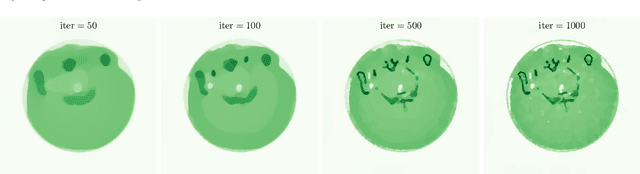
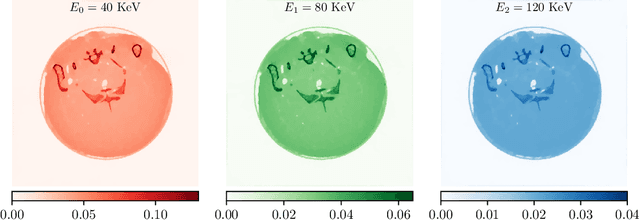
Jan 24, 2025Abstract:Electrical impedance tomography (EIT) is a non-invasive imaging method for recovering the internal conductivity of a physical body from electric boundary measurements. EIT combined with machine learning has shown promise for the classification of strokes. However, most previous works have used raw EIT voltage data as network inputs. We build upon a recent development which suggested the use of special noise-robust Virtual Hybrid Edge Detection (VHED) functions as network inputs, although that work used only highly simplified and mathematically ideal models. In this work we strengthen the case for the use of EIT, and VHED functions especially, for stroke classification. We design models with high detail and mathematical realism to test the use of VHED functions as inputs. Virtual patients are created using a physically detailed 2D head model which includes features known to create challenges in real-world imaging scenarios. Conductivity values are drawn from statistically realistic distributions, and phantoms are afflicted with either hemorrhagic or ischemic strokes of various shapes and sizes. Simulated noisy EIT electrode data, generated using the realistic Complete Electrode Model (CEM) as opposed to the mathematically ideal continuum model, is processed to obtain VHED functions. We compare the use of VHED functions as inputs against the alternative paradigm of using raw EIT voltages. Our results show that (i) stroke classification can be performed with high accuracy using 2D EIT data from physically detailed and mathematically realistic models, and (ii) in the presence of noise, VHED functions outperform raw data as network inputs.
Helsinki Speech Challenge 2024
Jun 06, 2024



Abstract:The Helsinki Speech Challenge 2024 (HSC2024) invites researchers to enhance and deconvolve speech audio recordings. We recorded a dataset that challenges participants to apply speech enhancement and inverse problems techniques to recorded speech data. This dataset includes paired samples of AI-generated clean speech and corresponding recordings, which feature varying levels of corruption, including frequency attenuation and reverberation. The challenge focuses on developing innovative deconvolution methods to accurately recover the original audio. The effectiveness of these methods will be quantitatively assessed using a speech recognition model, providing a relevant metric for evaluating enhancements in real-world scenarios.
TILT: topological interface recovery in limited-angle tomography
Oct 25, 2023



Abstract:A novel reconstruction method is introduced for the severely ill-posed inverse problem of limited-angle tomography. It is well known that, depending on the available measurement, angles specify a subset of the wavefront set of the unknown target, while some oriented singularities remain invisible in the data. Topological Interface recovery for Limited-angle Tomography, or TILT, is based on lifting the visible part of the wavefront set under a universal covering map. In the space provided, it is possible to connect the appropriate pieces of the lifted wavefront set correctly using dual-tree complex wavelets, a dedicated metric, and persistent homology. The result is not only a suggested invisible boundary but also a computational representation for all interfaces in the target.
Learning a microlocal priorfor limited-angle tomography
Dec 31, 2021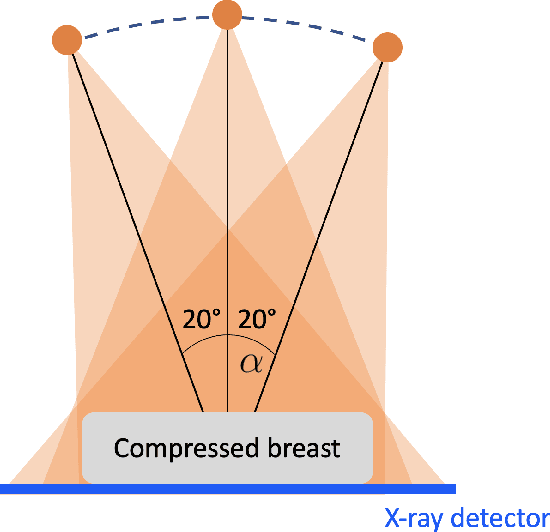
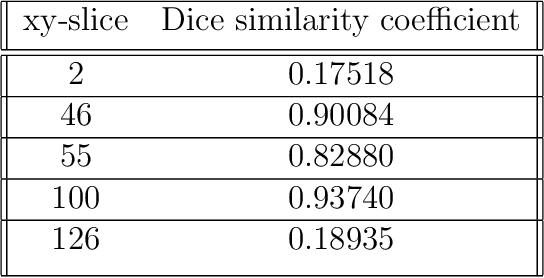
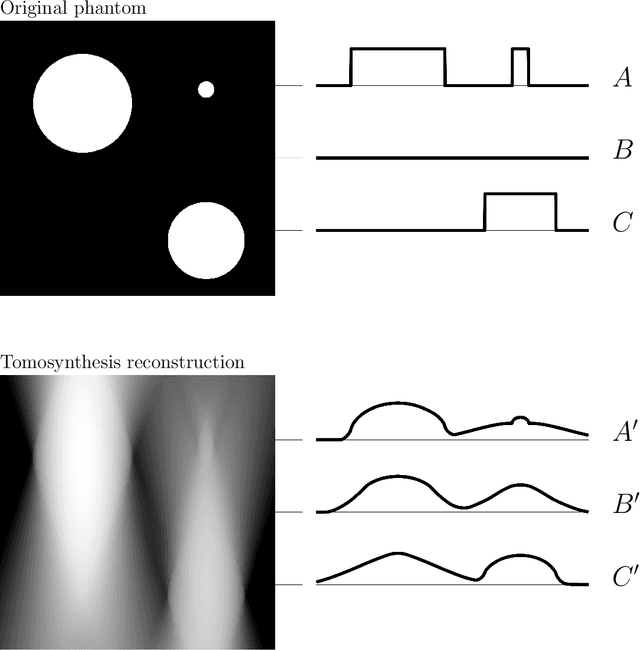
Abstract:Digital breast tomosynthesis is an ill posed inverse problem. In this paper, we provide a try to overcome the problem of stretching artefacts of DBT with the help of learning from the microlocal priors.
Helsinki Deblur Challenge 2021: description of photographic data
May 21, 2021

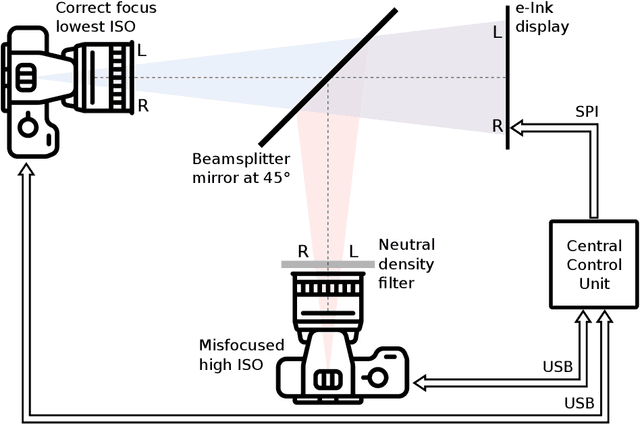
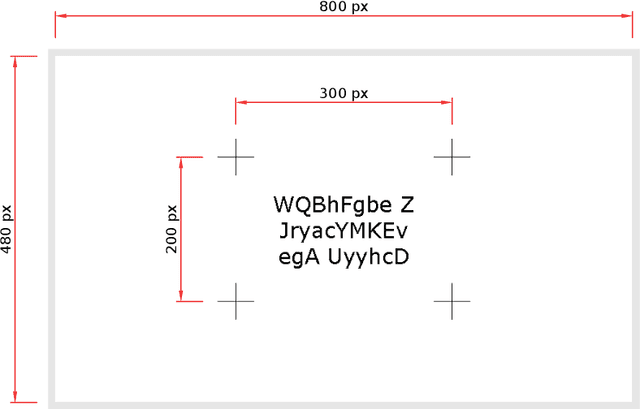
Abstract:The photographic dataset collected for the Helsinki Deblur Challenge 2021 (HDC2021) contains pairs of images taken by two identical cameras of the same target but with different conditions. One camera is always in focus and produces sharp and low-noise images the other camera produces blurred and noisy images as it is gradually more and more out of focus and has a higher ISO setting. Even though the dataset was designed and captured with the HDC2021 in mind it can be used for any testing and benchmarking of image deblurring algorithms. The data is available here: https://doi.org/10.5281/zenodo.477228
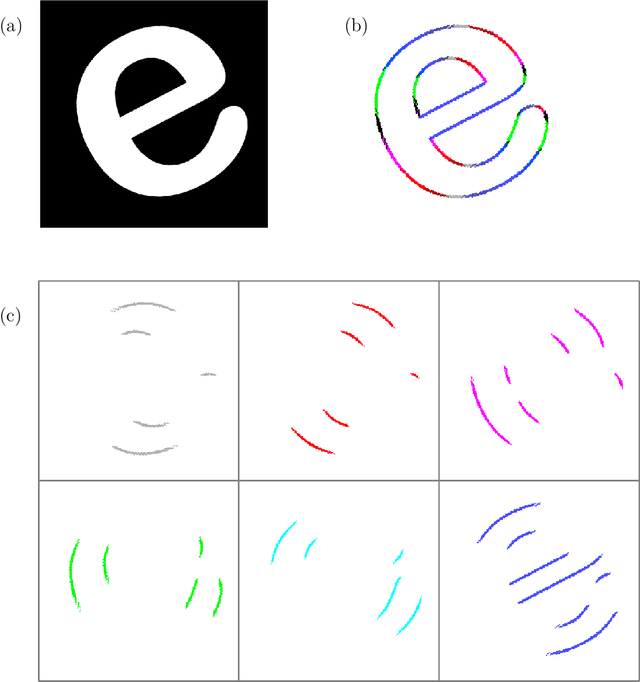
4D Dual-Tree Complex Wavelets for Time-Dependent Data
Mar 29, 2021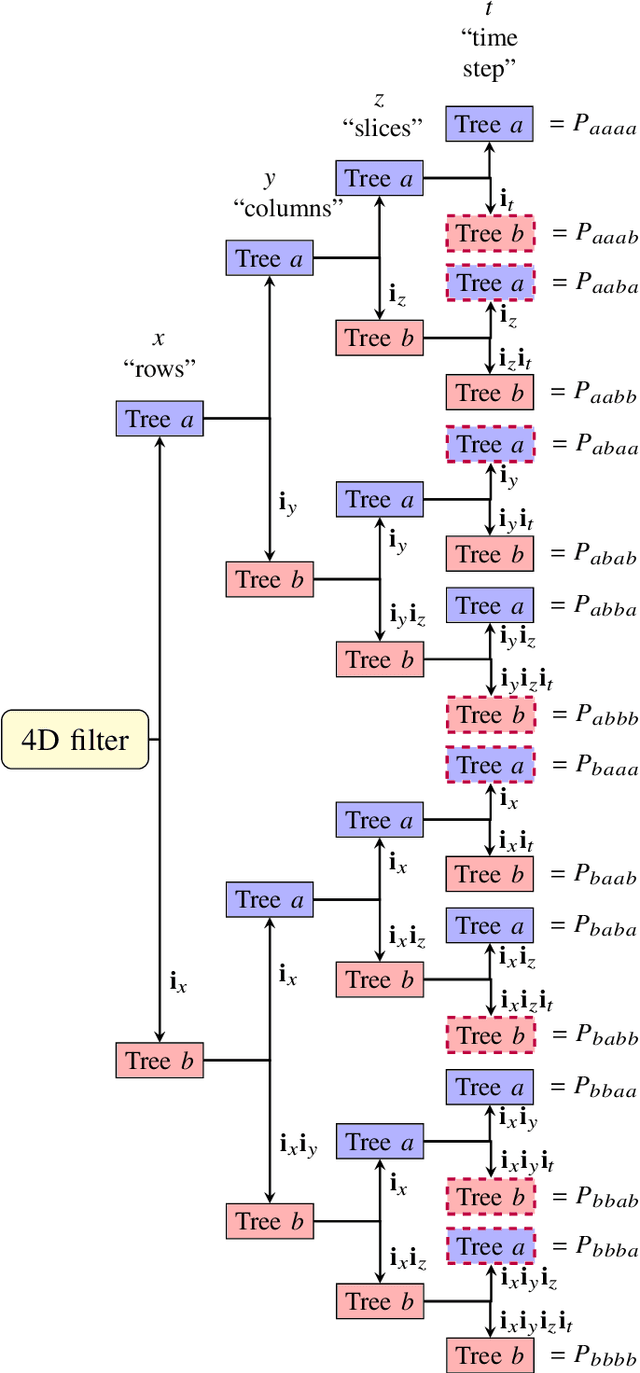


Abstract:The dual-tree complex wavelet transform (DT-$\mathbb{C}$WT) is extended to the 4D setting. Key properties of 4D DT-$\mathbb{C}$WT, such as directional sensitivity and shift-invariance, are discussed and illustrated in a tomographic application. The inverse problem of reconstructing a dynamic three-dimensional target from X-ray projection measurements can be formulated as 4D space-time tomography. The results suggest that 4D DT-$\mathbb{C}$WT offers simple implementations combined with useful theoretical properties for tomographic reconstruction.
Synergistic Multi-spectral CT Reconstruction with Directional Total Variation
Jan 06, 2021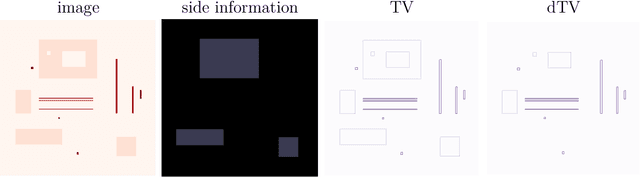
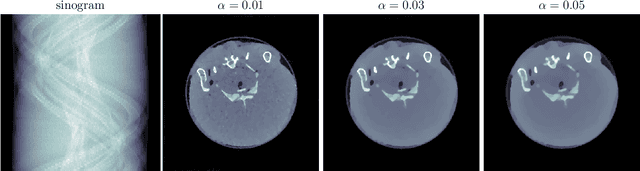
Abstract:This work considers synergistic multi-spectral CT reconstruction where information from all available energy channels is combined to improve the reconstruction of each individual channel, we propose to fuse this available data (represented by a single sinogram) to obtain a polyenergetic image which keeps structural information shared by the energy channels with increased signal-to-noise-ratio. This new image is used as prior information during the minimization process through the directional total variation. We analyze the use of directional total variation within variational regularization and iterative regularization. Our numerical results on simulated and experimental data show significant improvements in terms of image quality and in computational speed.
Deep neural networks for inverse problems with pseudodifferential operators: an application to limited-angle tomography
Jun 02, 2020
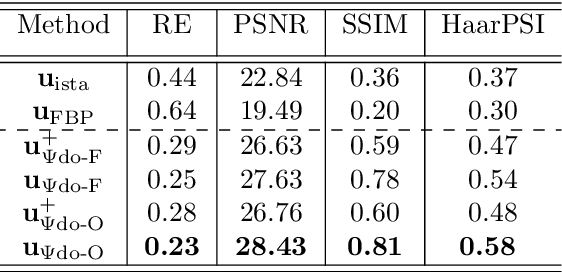
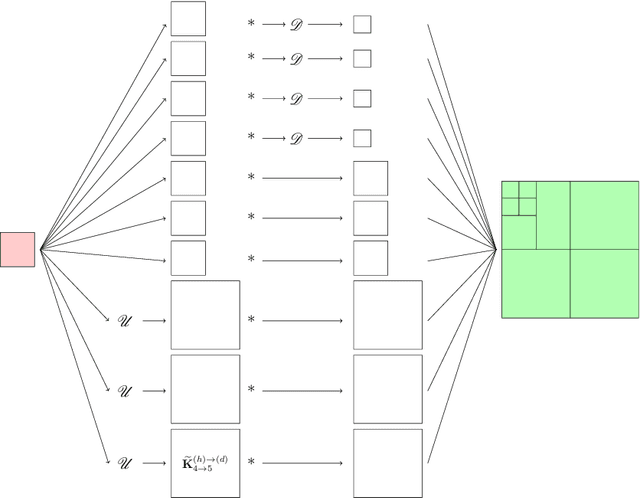
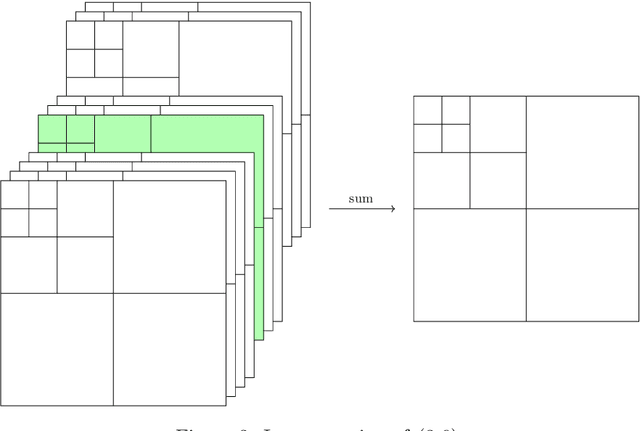
Abstract:We propose a novel convolutional neural network (CNN), called $\Psi$DONet, designed for learning pseudodifferential operators ($\Psi$DOs) in the context of linear inverse problems. Our starting point is the Iterative Soft Thresholding Algorithm (ISTA), a well-known algorithm to solve sparsity-promoting minimization problems. We show that, under rather general assumptions on the forward operator, the unfolded iterations of ISTA can be interpreted as the successive layers of a CNN, which in turn provides fairly general network architectures that, for a specific choice of the parameters involved, allow to reproduce ISTA, or a perturbation of ISTA for which we can bound the coefficients of the filters. Our case study is the limited-angle X-ray transform and its application to limited-angle computed tomography (LA-CT). In particular, we prove that, in the case of LA-CT, the operations of upscaling, downscaling and convolution, which characterize our $\Psi$DONet and most deep learning schemes, can be exactly determined by combining the convolutional nature of the limited angle X-ray transform and basic properties defining an orthogonal wavelet system. We test two different implementations of $\Psi$DONet on simulated data from limited-angle geometry, generated from the ellipse data set. Both implementations provide equally good and noteworthy preliminary results, showing the potential of the approach we propose and paving the way to applying the same idea to other convolutional operators which are $\Psi$DOs or Fourier integral operators.
Photographic dataset: playing cards
Jan 25, 2017



Abstract:This is a photographic dataset collected for testing image processing algorithms. The idea is to have images that can exploit the properties of total variation, therefore a set of playing cards was distributed on the scene. The dataset is made available at www.fips.fi/photographic_dataset2.php
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge