Deep neural networks for inverse problems with pseudodifferential operators: an application to limited-angle tomography

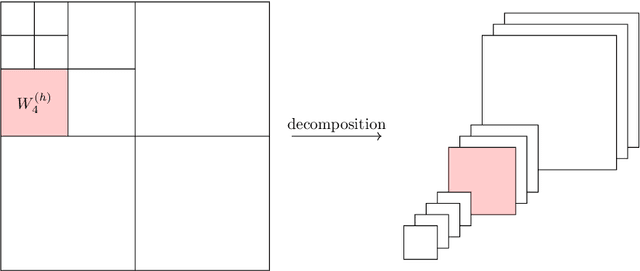
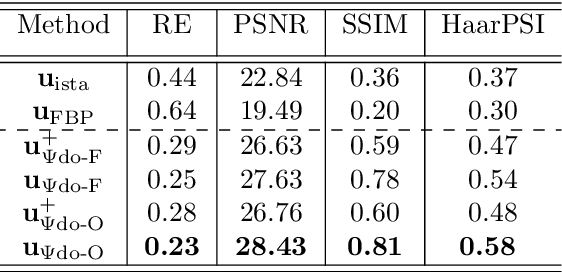
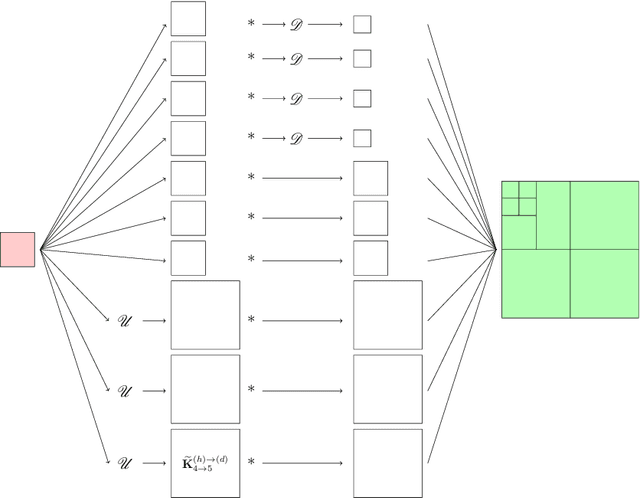
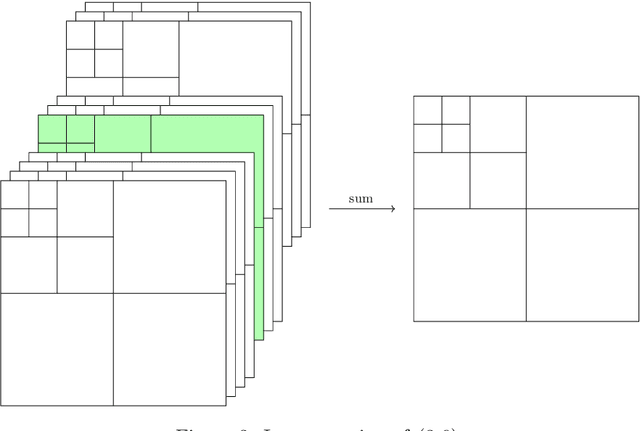
We propose a novel convolutional neural network (CNN), called $\Psi$DONet, designed for learning pseudodifferential operators ($\Psi$DOs) in the context of linear inverse problems. Our starting point is the Iterative Soft Thresholding Algorithm (ISTA), a well-known algorithm to solve sparsity-promoting minimization problems. We show that, under rather general assumptions on the forward operator, the unfolded iterations of ISTA can be interpreted as the successive layers of a CNN, which in turn provides fairly general network architectures that, for a specific choice of the parameters involved, allow to reproduce ISTA, or a perturbation of ISTA for which we can bound the coefficients of the filters. Our case study is the limited-angle X-ray transform and its application to limited-angle computed tomography (LA-CT). In particular, we prove that, in the case of LA-CT, the operations of upscaling, downscaling and convolution, which characterize our $\Psi$DONet and most deep learning schemes, can be exactly determined by combining the convolutional nature of the limited angle X-ray transform and basic properties defining an orthogonal wavelet system. We test two different implementations of $\Psi$DONet on simulated data from limited-angle geometry, generated from the ellipse data set. Both implementations provide equally good and noteworthy preliminary results, showing the potential of the approach we propose and paving the way to applying the same idea to other convolutional operators which are $\Psi$DOs or Fourier integral operators.

Mise en abyme with artificial intelligence: how to predict the accuracy of NN, applied to hyper-parameter tuning

In the context of deep learning, the costliest phase from a computational point of view is the full training of the learning algorithm. However, this process is to be used a significant number of times during the design of a new artificial neural network, leading therefore to extremely expensive operations. Here, we propose a low-cost strategy to predict the accuracy of the algorithm, based only on its initial behaviour. To do so, we train the network of interest up to convergence several times, modifying its characteristics at each training. The initial and final accuracies observed during this beforehand process are stored in a database. We then make use of both curve fitting and Support Vector Machines techniques, the latter being trained on the created database, to predict the accuracy of the network, given its accuracy on the primary iterations of its learning. This approach can be of particular interest when the space of the characteristics of the network is notably large or when its full training is highly time-consuming. The results we obtained are promising and encouraged us to apply this strategy to a topical issue: hyper-parameter optimisation (HO). In particular, we focused on the HO of a convolutional neural network for the classification of the databases MNIST and CIFAR-10. By using our method of prediction, and an algorithm implemented by us for a probabilistic exploration of the hyper-parameter space, we were able to find the hyper-parameter settings corresponding to the optimal accuracies already known in literature, at a quite low-cost.