TILT: topological interface recovery in limited-angle tomography

A novel reconstruction method is introduced for the severely ill-posed inverse problem of limited-angle tomography. It is well known that, depending on the available measurement, angles specify a subset of the wavefront set of the unknown target, while some oriented singularities remain invisible in the data. Topological Interface recovery for Limited-angle Tomography, or TILT, is based on lifting the visible part of the wavefront set under a universal covering map. In the space provided, it is possible to connect the appropriate pieces of the lifted wavefront set correctly using dual-tree complex wavelets, a dedicated metric, and persistent homology. The result is not only a suggested invisible boundary but also a computational representation for all interfaces in the target.

Deep Invertible Approximation of Topologically Rich Maps between Manifolds

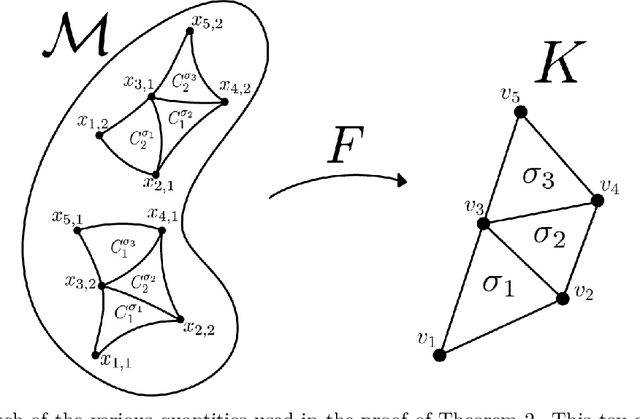
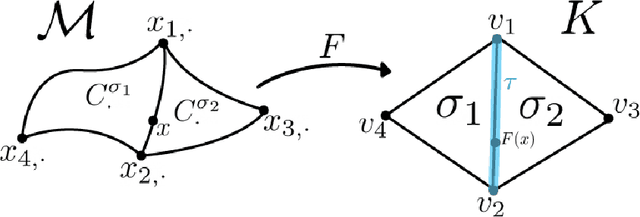
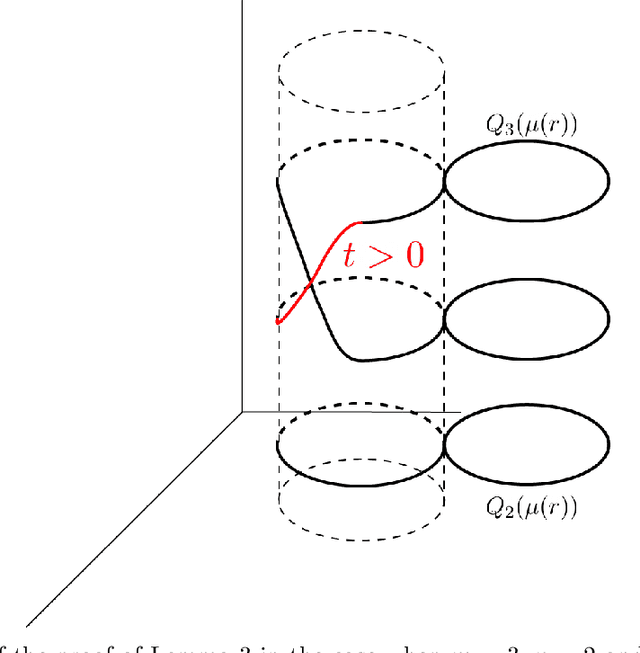
How can we design neural networks that allow for stable universal approximation of maps between topologically interesting manifolds? The answer is with a coordinate projection. Neural networks based on topological data analysis (TDA) use tools such as persistent homology to learn topological signatures of data and stabilize training but may not be universal approximators or have stable inverses. Other architectures universally approximate data distributions on submanifolds but only when the latter are given by a single chart, making them unable to learn maps that change topology. By exploiting the topological parallels between locally bilipschitz maps, covering spaces, and local homeomorphisms, and by using universal approximation arguments from machine learning, we find that a novel network of the form $\mathcal{T} \circ p \circ \mathcal{E}$, where $\mathcal{E}$ is an injective network, $p$ a fixed coordinate projection, and $\mathcal{T}$ a bijective network, is a universal approximator of local diffeomorphisms between compact smooth submanifolds embedded in $\mathbb{R}^n$. We emphasize the case when the target map changes topology. Further, we find that by constraining the projection $p$, multivalued inversions of our networks can be computed without sacrificing universality. As an application, we show that learning a group invariant function with unknown group action naturally reduces to the question of learning local diffeomorphisms for finite groups. Our theory permits us to recover orbits of the group action. We also outline possible extensions of our architecture to address molecular imaging of molecules with symmetries. Finally, our analysis informs the choice of topologically expressive starting spaces in generative problems.