Joint Cryo-ET Alignment and Reconstruction with Neural Deformation Fields

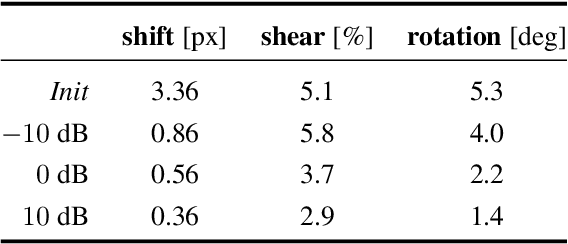
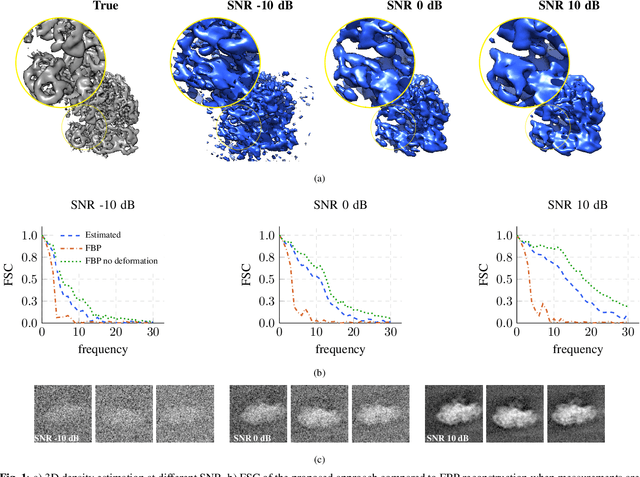
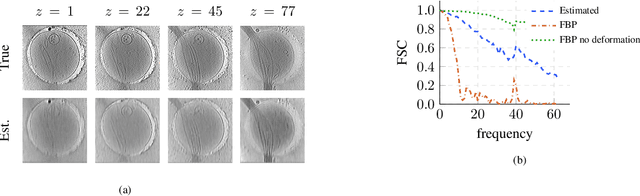
We propose a framework to jointly determine the deformation parameters and reconstruct the unknown volume in electron cryotomography (CryoET). CryoET aims to reconstruct three-dimensional biological samples from two-dimensional projections. A major challenge is that we can only acquire projections for a limited range of tilts, and that each projection undergoes an unknown deformation during acquisition. Not accounting for these deformations results in poor reconstruction. The existing CryoET software packages attempt to align the projections, often in a workflow which uses manual feedback. Our proposed method sidesteps this inconvenience by automatically computing a set of undeformed projections while simultaneously reconstructing the unknown volume. We achieve this by learning a continuous representation of the undeformed measurements and deformation parameters. We show that our approach enables the recovery of high-frequency details that are destroyed without accounting for deformations.

Deep Invertible Approximation of Topologically Rich Maps between Manifolds

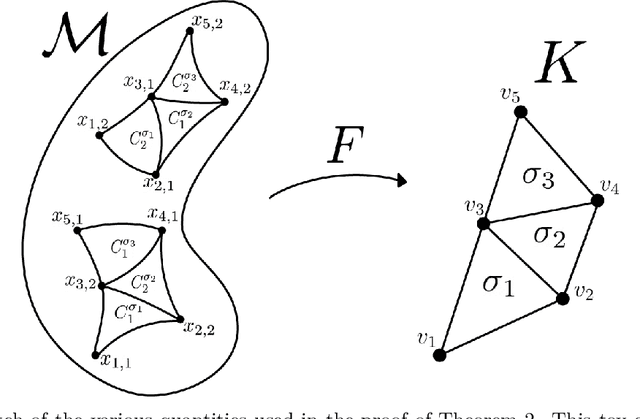
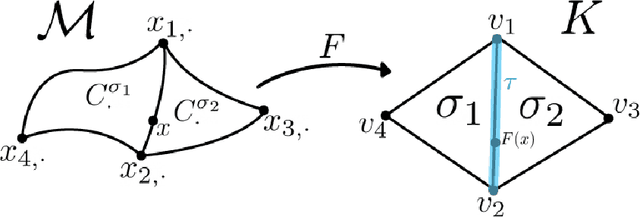
How can we design neural networks that allow for stable universal approximation of maps between topologically interesting manifolds? The answer is with a coordinate projection. Neural networks based on topological data analysis (TDA) use tools such as persistent homology to learn topological signatures of data and stabilize training but may not be universal approximators or have stable inverses. Other architectures universally approximate data distributions on submanifolds but only when the latter are given by a single chart, making them unable to learn maps that change topology. By exploiting the topological parallels between locally bilipschitz maps, covering spaces, and local homeomorphisms, and by using universal approximation arguments from machine learning, we find that a novel network of the form $\mathcal{T} \circ p \circ \mathcal{E}$, where $\mathcal{E}$ is an injective network, $p$ a fixed coordinate projection, and $\mathcal{T}$ a bijective network, is a universal approximator of local diffeomorphisms between compact smooth submanifolds embedded in $\mathbb{R}^n$. We emphasize the case when the target map changes topology. Further, we find that by constraining the projection $p$, multivalued inversions of our networks can be computed without sacrificing universality. As an application, we show that learning a group invariant function with unknown group action naturally reduces to the question of learning local diffeomorphisms for finite groups. Our theory permits us to recover orbits of the group action. We also outline possible extensions of our architecture to address molecular imaging of molecules with symmetries. Finally, our analysis informs the choice of topologically expressive starting spaces in generative problems.

On Procrustes Analysis in Hyperbolic Space

Congruent Procrustes analysis aims to find the best matching between two point sets through rotation, reflection and translation. We formulate the Procrustes problem for hyperbolic spaces, review the canonical definition of the center of point sets, and give a closed form solution for the optimal isometry for noise-free measurements. We also analyze the performance of the proposed method under measurement noise.

Look, no Beacons! Optimal All-in-One EchoSLAM

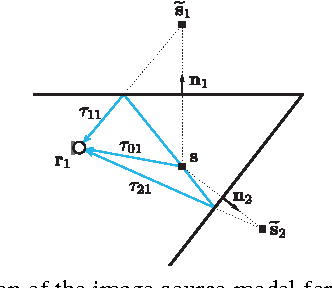
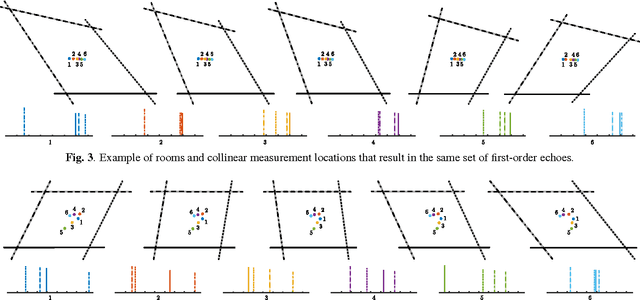
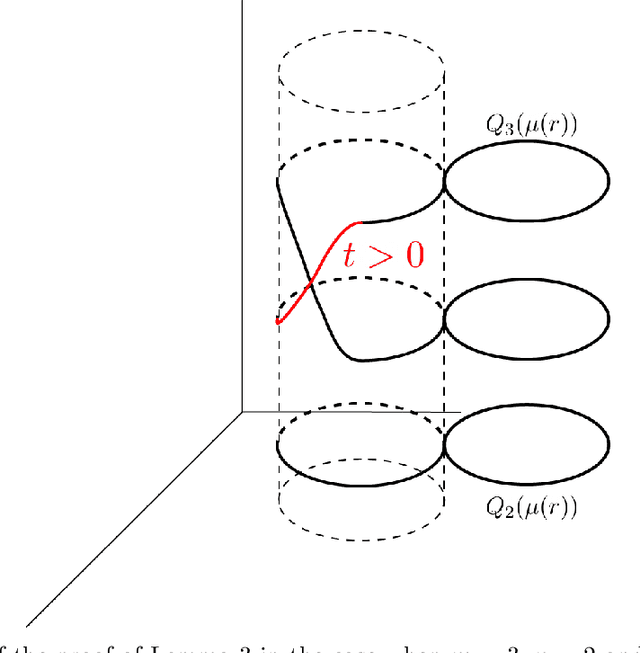
We study the problem of simultaneously reconstructing a polygonal room and a trajectory of a device equipped with a (nearly) collocated omnidirectional source and receiver. The device measures arrival times of echoes of pulses emitted by the source and picked up by the receiver. No prior knowledge about the device's trajectory is required. Most existing approaches addressing this problem assume multiple sources or receivers, or they assume that some of these are static, serving as beacons. Unlike earlier approaches, we take into account the measurement noise and various constraints on the geometry by formulating the solution as a minimizer of a cost function similar to \emph{stress} in multidimensional scaling. We study uniqueness of the reconstruction from first-order echoes, and we show that in addition to the usual invariance to rigid motions, new ambiguities arise for important classes of rooms and trajectories. We support our theoretical developments with a number of numerical experiments.