Look, no Beacons! Optimal All-in-One EchoSLAM

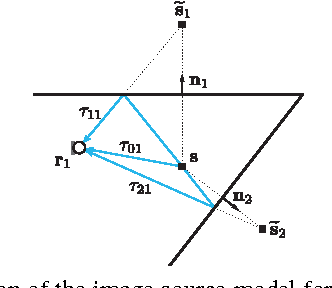
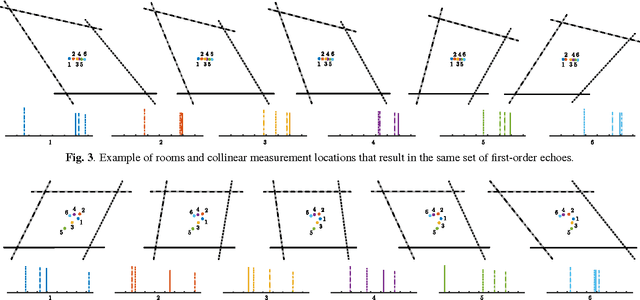
We study the problem of simultaneously reconstructing a polygonal room and a trajectory of a device equipped with a (nearly) collocated omnidirectional source and receiver. The device measures arrival times of echoes of pulses emitted by the source and picked up by the receiver. No prior knowledge about the device's trajectory is required. Most existing approaches addressing this problem assume multiple sources or receivers, or they assume that some of these are static, serving as beacons. Unlike earlier approaches, we take into account the measurement noise and various constraints on the geometry by formulating the solution as a minimizer of a cost function similar to \emph{stress} in multidimensional scaling. We study uniqueness of the reconstruction from first-order echoes, and we show that in addition to the usual invariance to rigid motions, new ambiguities arise for important classes of rooms and trajectories. We support our theoretical developments with a number of numerical experiments.