Automated Deep Aberration Detection from Chromosome Karyotype Images

Chromosome analysis is essential for diagnosing genetic disorders. For hematologic malignancies, identification of somatic clonal aberrations by karyotype analysis remains the standard of care. However, karyotyping is costly and time-consuming because of the largely manual process and the expertise required in identifying and annotating aberrations. Efforts to automate karyotype analysis to date fell short in aberration detection. Using a training set of ~10k patient specimens and ~50k karyograms from over 5 years from the Fred Hutchinson Cancer Center, we created a labeled set of images representing individual chromosomes. These individual chromosomes were used to train and assess deep learning models for classifying the 24 human chromosomes and identifying chromosomal aberrations. The top-accuracy models utilized the recently introduced Topological Vision Transformers (TopViTs) with 2-level-block-Toeplitz masking, to incorporate structural inductive bias. TopViT outperformed CNN (Inception) models with >99.3% accuracy for chromosome identification, and exhibited accuracies >99% for aberration detection in most aberrations. Notably, we were able to show high-quality performance even in "few shot" learning scenarios. Incorporating the definition of clonality substantially improved both precision and recall (sensitivity). When applied to "zero shot" scenarios, the model captured aberrations without training, with perfect precision at >50% recall. Together these results show that modern deep learning models can approach expert-level performance for chromosome aberration detection. To our knowledge, this is the first study demonstrating the downstream effectiveness of TopViTs. These results open up exciting opportunities for not only expediting patient results but providing a scalable technology for early screening of low-abundance chromosomal lesions.

Joint Cryo-ET Alignment and Reconstruction with Neural Deformation Fields

We propose a framework to jointly determine the deformation parameters and reconstruct the unknown volume in electron cryotomography (CryoET). CryoET aims to reconstruct three-dimensional biological samples from two-dimensional projections. A major challenge is that we can only acquire projections for a limited range of tilts, and that each projection undergoes an unknown deformation during acquisition. Not accounting for these deformations results in poor reconstruction. The existing CryoET software packages attempt to align the projections, often in a workflow which uses manual feedback. Our proposed method sidesteps this inconvenience by automatically computing a set of undeformed projections while simultaneously reconstructing the unknown volume. We achieve this by learning a continuous representation of the undeformed measurements and deformation parameters. We show that our approach enables the recovery of high-frequency details that are destroyed without accounting for deformations.

Differentiable Uncalibrated Imaging

We propose a differentiable imaging framework to address uncertainty in measurement coordinates such as sensor locations and projection angles. We formulate the problem as measurement interpolation at unknown nodes supervised through the forward operator. To solve it we apply implicit neural networks, also known as neural fields, which are naturally differentiable with respect to the input coordinates. We also develop differentiable spline interpolators which perform as well as neural networks, require less time to optimize and have well-understood properties. Differentiability is key as it allows us to jointly fit a measurement representation, optimize over the uncertain measurement coordinates, and perform image reconstruction which in turn ensures consistent calibration. We apply our approach to 2D and 3D computed tomography and show that it produces improved reconstructions compared to baselines that do not account for the lack of calibration. The flexibility of the proposed framework makes it easy to apply to almost arbitrary imaging problems.

Conditional Injective Flows for Bayesian Imaging

Most deep learning models for computational imaging regress a single reconstructed image. In practice, however, ill-posedness, nonlinearity, model mismatch, and noise often conspire to make such point estimates misleading or insufficient. The Bayesian approach models images and (noisy) measurements as jointly distributed random vectors and aims to approximate the posterior distribution of unknowns. Recent variational inference methods based on conditional normalizing flows are a promising alternative to traditional MCMC methods, but they come with drawbacks: excessive memory and compute demands for moderate to high resolution images and underwhelming performance on hard nonlinear problems. In this work, we propose C-Trumpets -- conditional injective flows specifically designed for imaging problems, which greatly diminish these challenges. Injectivity reduces memory footprint and training time while low-dimensional latent space together with architectural innovations like fixed-volume-change layers and skip-connection revnet layers, C-Trumpets outperform regular conditional flow models on a variety of imaging and image restoration tasks, including limited-view CT and nonlinear inverse scattering, with a lower compute and memory budget. C-Trumpets enable fast approximation of point estimates like MMSE or MAP as well as physically-meaningful uncertainty quantification.

Trumpets: Injective Flows for Inference and Inverse Problems

We propose injective generative models called Trumpets that generalize invertible normalizing flows. The proposed generators progressively increase dimension from a low-dimensional latent space. We demonstrate that Trumpets can be trained orders of magnitudes faster than standard flows while yielding samples of comparable or better quality. They retain many of the advantages of the standard flows such as training based on maximum likelihood and a fast, exact inverse of the generator. Since Trumpets are injective and have fast inverses, they can be effectively used for downstream Bayesian inference. To wit, we use Trumpet priors for maximum a posteriori estimation in the context of image reconstruction from compressive measurements, outperforming competitive baselines in terms of reconstruction quality and speed. We then propose an efficient method for posterior characterization and uncertainty quantification with Trumpets by taking advantage of the low-dimensional latent space.

Globally Injective ReLU Networks

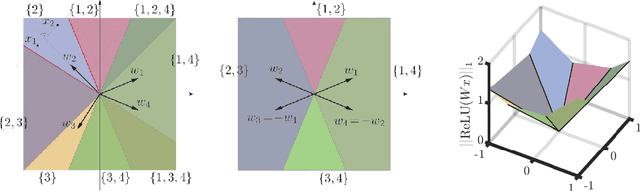
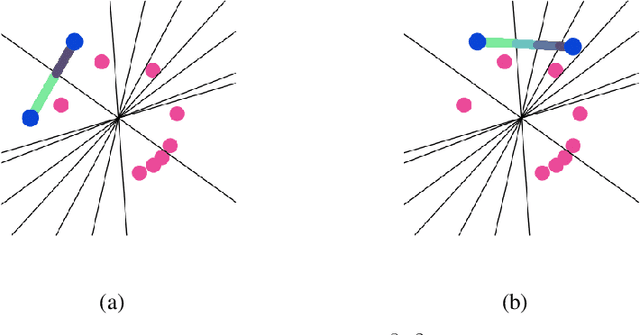
We study injective ReLU neural networks. Injectivity plays an important role in generative models where it facilitates inference; in inverse problems with generative priors it is a precursor to well posedness. We establish sharp conditions for injectivity of ReLU layers and networks, both fully connected and convolutional. We make no architectural assumptions beyond the ReLU activations so our results apply to a very general class of neural networks. We show through a layer-wise analysis that an expansivity factor of two is necessary for injectivity; we also show sufficiency by constructing weight matrices which guarantee injectivity. Further, we show that global injectivity with iid Gaussian matrices, a commonly used tractable model, requires considerably larger expansivity which might seem counterintuitive. We then derive the inverse Lipschitz constants and study the approximation-theoretic properties of injective neural networks. Using arguments from differential topology we prove that, under mild technical conditions, any Lipschitz map can be approximated by an injective neural network. This justifies the use of injective neural networks in problems which a priori do not require injectivity. Our results establish a theoretical basis for the study of nonlinear inverse and inference problems using neural networks.

Learning the geometry of wave-based imaging

We propose a general deep learning architecture for wave-based imaging problems. A key difficulty in imaging problems with varying background wave speed is that the medium "bends" the waves differently depending on their position and direction. This space-bending geometry makes the equivariance to translations of convolutional networks an undesired inductive bias. We build an interpretable architecture based on wave physics, as captured by the Fourier integral operators (FIOs). FIOs appear in the description of a wide range of wave-based imaging modalities, from seismology and radar to Doppler and ultrasound. Their geometry is characterized by a canonical relation which governs the propagation of singularities. We learn this geometry via optimal transport in the wave packet representation. The proposed FIONet performs significantly better than the usual baselines on a number of inverse problems, especially in out-of-distribution tests.

Random mesh projectors for inverse problems

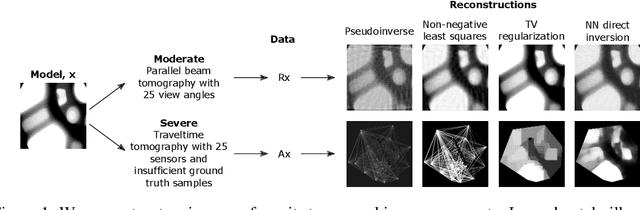
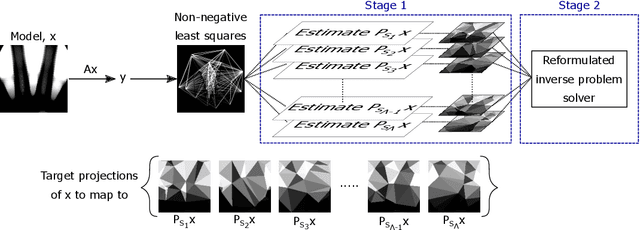
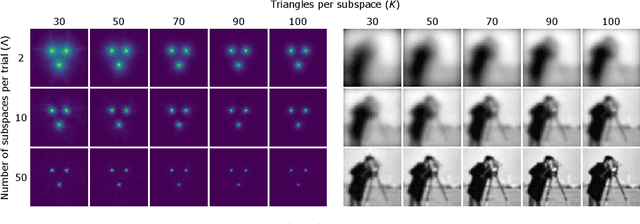
We propose a new learning-based approach to solve ill-posed inverse problems in imaging. We address the case where ground truth training samples are rare and the problem is severely ill-posed - both because of the underlying physics and because we can only get few measurements. This setting is common in geophysical imaging and remote sensing. We show that in this case the common approach to directly learn the mapping from the measured data to the reconstruction becomes unstable. Instead, we propose to first learn an ensemble of simpler mappings from the data to projections of the unknown image into random piecewise-constant subspaces. We then combine the projections to form a final reconstruction by solving a deconvolution-like problem. We show experimentally the proposed method is more robust to measurement noise and corruptions not seen during training than a directly learned inverse.