Mixture of Experts Soften the Curse of Dimensionality in Operator Learning

In this paper, we construct a mixture of neural operators (MoNOs) between function spaces whose complexity is distributed over a network of expert neural operators (NOs), with each NO satisfying parameter scaling restrictions. Our main result is a \textit{distributed} universal approximation theorem guaranteeing that any Lipschitz non-linear operator between $L^2([0,1]^d)$ spaces can be approximated uniformly over the Sobolev unit ball therein, to any given $\varepsilon>0$ accuracy, by an MoNO while satisfying the constraint that: each expert NO has a depth, width, and rank of $\mathcal{O}(\varepsilon^{-1})$. Naturally, our result implies that the required number of experts must be large, however, each NO is guaranteed to be small enough to be loadable into the active memory of most computers for reasonable accuracies $\varepsilon$. During our analysis, we also obtain new quantitative expression rates for classical NOs approximating uniformly continuous non-linear operators uniformly on compact subsets of $L^2([0,1]^d)$.

Neural multi-event forecasting on spatio-temporal point processes using probabilistically enriched transformers

Predicting discrete events in time and space has many scientific applications, such as predicting hazardous earthquakes and outbreaks of infectious diseases. History-dependent spatio-temporal Hawkes processes are often used to mathematically model these point events. However, previous approaches have faced numerous challenges, particularly when attempting to forecast one or multiple future events. In this work, we propose a new neural architecture for multi-event forecasting of spatio-temporal point processes, utilizing transformers, augmented with normalizing flows and probabilistic layers. Our network makes batched predictions of complex history-dependent spatio-temporal distributions of future discrete events, achieving state-of-the-art performance on a variety of benchmark datasets including the South California Earthquakes, Citibike, Covid-19, and Hawkes synthetic pinwheel datasets. More generally, we illustrate how our network can be applied to any dataset of discrete events with associated markers, even when no underlying physics is known.

Deep Invertible Approximation of Topologically Rich Maps between Manifolds

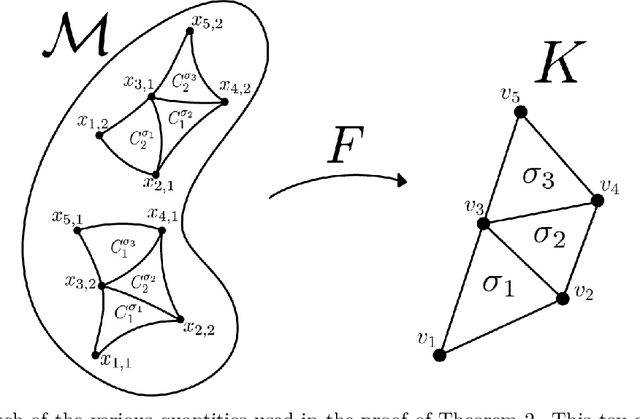
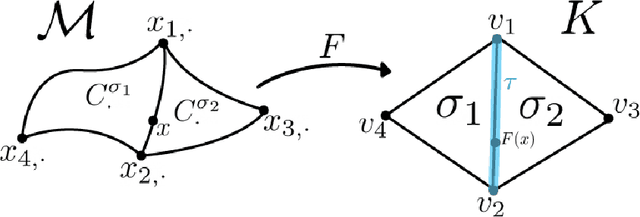
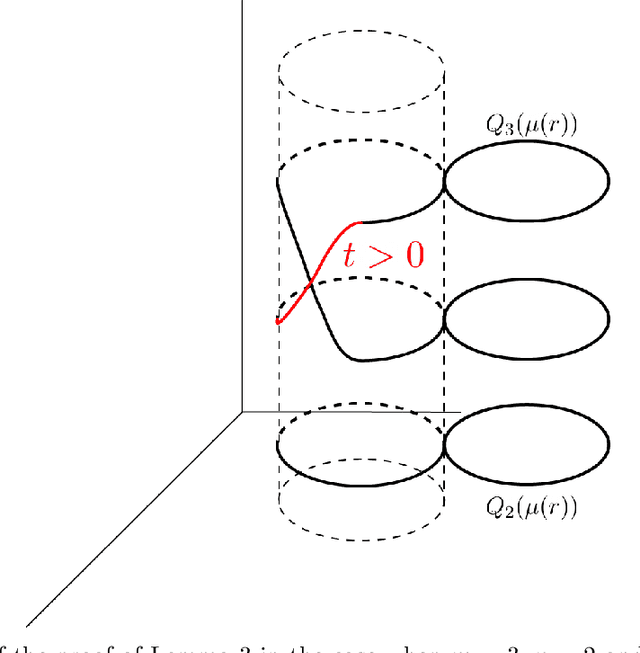
How can we design neural networks that allow for stable universal approximation of maps between topologically interesting manifolds? The answer is with a coordinate projection. Neural networks based on topological data analysis (TDA) use tools such as persistent homology to learn topological signatures of data and stabilize training but may not be universal approximators or have stable inverses. Other architectures universally approximate data distributions on submanifolds but only when the latter are given by a single chart, making them unable to learn maps that change topology. By exploiting the topological parallels between locally bilipschitz maps, covering spaces, and local homeomorphisms, and by using universal approximation arguments from machine learning, we find that a novel network of the form $\mathcal{T} \circ p \circ \mathcal{E}$, where $\mathcal{E}$ is an injective network, $p$ a fixed coordinate projection, and $\mathcal{T}$ a bijective network, is a universal approximator of local diffeomorphisms between compact smooth submanifolds embedded in $\mathbb{R}^n$. We emphasize the case when the target map changes topology. Further, we find that by constraining the projection $p$, multivalued inversions of our networks can be computed without sacrificing universality. As an application, we show that learning a group invariant function with unknown group action naturally reduces to the question of learning local diffeomorphisms for finite groups. Our theory permits us to recover orbits of the group action. We also outline possible extensions of our architecture to address molecular imaging of molecules with symmetries. Finally, our analysis informs the choice of topologically expressive starting spaces in generative problems.

Conditional Injective Flows for Bayesian Imaging

Most deep learning models for computational imaging regress a single reconstructed image. In practice, however, ill-posedness, nonlinearity, model mismatch, and noise often conspire to make such point estimates misleading or insufficient. The Bayesian approach models images and (noisy) measurements as jointly distributed random vectors and aims to approximate the posterior distribution of unknowns. Recent variational inference methods based on conditional normalizing flows are a promising alternative to traditional MCMC methods, but they come with drawbacks: excessive memory and compute demands for moderate to high resolution images and underwhelming performance on hard nonlinear problems. In this work, we propose C-Trumpets -- conditional injective flows specifically designed for imaging problems, which greatly diminish these challenges. Injectivity reduces memory footprint and training time while low-dimensional latent space together with architectural innovations like fixed-volume-change layers and skip-connection revnet layers, C-Trumpets outperform regular conditional flow models on a variety of imaging and image restoration tasks, including limited-view CT and nonlinear inverse scattering, with a lower compute and memory budget. C-Trumpets enable fast approximation of point estimates like MMSE or MAP as well as physically-meaningful uncertainty quantification.

Universal Joint Approximation of Manifolds and Densities by Simple Injective Flows

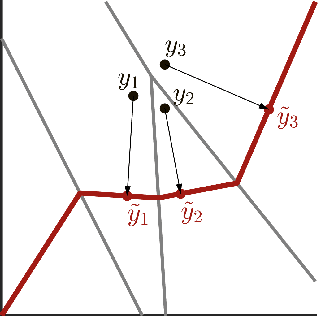
We analyze neural networks composed of bijective flows and injective expansive elements. We find that such networks universally approximate a large class of manifolds simultaneously with densities supported on them. Among others, our results apply to the well-known coupling and autoregressive flows. We build on the work of Teshima et al. 2020 on bijective flows and study injective architectures proposed in Brehmer et al. 2020 and Kothari et al. 2021. Our results leverage a new theoretical device called the embedding gap, which measures how far one continuous manifold is from embedding another. We relate the embedding gap to a relaxation of universally we call the manifold embedding property, capturing the geometric part of universality. Our proof also establishes that optimality of a network can be established in reverse, resolving a conjecture made in Brehmer et al. 2020 and opening the door for simple layer-wise training schemes. Finally, we show that the studied networks admit an exact layer-wise projection result, Bayesian uncertainty quantification, and black-box recovery of network weights.

Trumpets: Injective Flows for Inference and Inverse Problems

We propose injective generative models called Trumpets that generalize invertible normalizing flows. The proposed generators progressively increase dimension from a low-dimensional latent space. We demonstrate that Trumpets can be trained orders of magnitudes faster than standard flows while yielding samples of comparable or better quality. They retain many of the advantages of the standard flows such as training based on maximum likelihood and a fast, exact inverse of the generator. Since Trumpets are injective and have fast inverses, they can be effectively used for downstream Bayesian inference. To wit, we use Trumpet priors for maximum a posteriori estimation in the context of image reconstruction from compressive measurements, outperforming competitive baselines in terms of reconstruction quality and speed. We then propose an efficient method for posterior characterization and uncertainty quantification with Trumpets by taking advantage of the low-dimensional latent space.

Globally Injective ReLU Networks

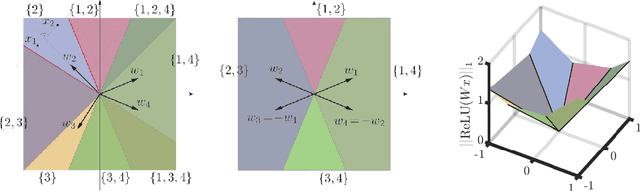
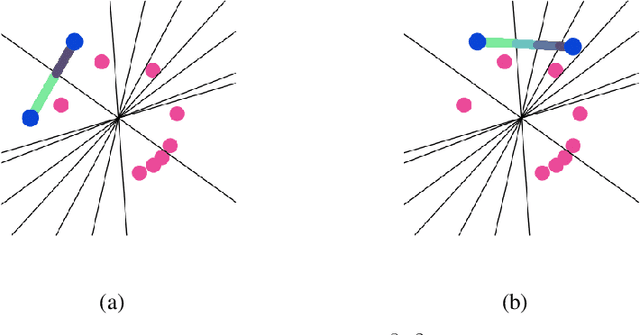
We study injective ReLU neural networks. Injectivity plays an important role in generative models where it facilitates inference; in inverse problems with generative priors it is a precursor to well posedness. We establish sharp conditions for injectivity of ReLU layers and networks, both fully connected and convolutional. We make no architectural assumptions beyond the ReLU activations so our results apply to a very general class of neural networks. We show through a layer-wise analysis that an expansivity factor of two is necessary for injectivity; we also show sufficiency by constructing weight matrices which guarantee injectivity. Further, we show that global injectivity with iid Gaussian matrices, a commonly used tractable model, requires considerably larger expansivity which might seem counterintuitive. We then derive the inverse Lipschitz constants and study the approximation-theoretic properties of injective neural networks. Using arguments from differential topology we prove that, under mild technical conditions, any Lipschitz map can be approximated by an injective neural network. This justifies the use of injective neural networks in problems which a priori do not require injectivity. Our results establish a theoretical basis for the study of nonlinear inverse and inference problems using neural networks.

Learning the geometry of wave-based imaging

We propose a general deep learning architecture for wave-based imaging problems. A key difficulty in imaging problems with varying background wave speed is that the medium "bends" the waves differently depending on their position and direction. This space-bending geometry makes the equivariance to translations of convolutional networks an undesired inductive bias. We build an interpretable architecture based on wave physics, as captured by the Fourier integral operators (FIOs). FIOs appear in the description of a wide range of wave-based imaging modalities, from seismology and radar to Doppler and ultrasound. Their geometry is characterized by a canonical relation which governs the propagation of singularities. We learn this geometry via optimal transport in the wave packet representation. The proposed FIONet performs significantly better than the usual baselines on a number of inverse problems, especially in out-of-distribution tests.

Learning Schatten--Von Neumann Operators

We study the learnability of a class of compact operators known as Schatten--von Neumann operators. These operators between infinite-dimensional function spaces play a central role in a variety of applications in learning theory and inverse problems. We address the question of sample complexity of learning Schatten-von Neumann operators and provide an upper bound on the number of measurements required for the empirical risk minimizer to generalize with arbitrary precision and probability, as a function of class parameter $p$. Our results give generalization guarantees for regression of infinite-dimensional signals from infinite-dimensional data. Next, we adapt the representer theorem of Abernethy \emph{et al.} to show that empirical risk minimization over an a priori infinite-dimensional, non-compact set, can be converted to a convex finite dimensional optimization problem over a compact set. In summary, the class of $p$-Schatten--von Neumann operators is probably approximately correct (PAC)-learnable via a practical convex program for any $p < \infty$.