Can neural operators always be continuously discretized?

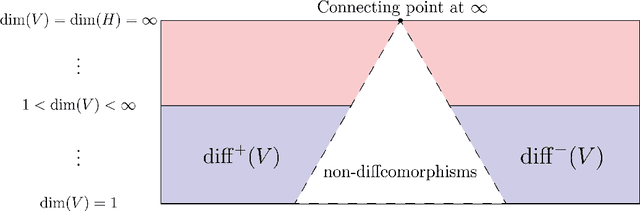
We consider the problem of discretization of neural operators between Hilbert spaces in a general framework including skip connections. We focus on bijective neural operators through the lens of diffeomorphisms in infinite dimensions. Framed using category theory, we give a no-go theorem that shows that diffeomorphisms between Hilbert spaces or Hilbert manifolds may not admit any continuous approximations by diffeomorphisms on finite-dimensional spaces, even if the approximations are nonlinear. The natural way out is the introduction of strongly monotone diffeomorphisms and layerwise strongly monotone neural operators which have continuous approximations by strongly monotone diffeomorphisms on finite-dimensional spaces. For these, one can guarantee discretization invariance, while ensuring that finite-dimensional approximations converge not only as sequences of functions, but that their representations converge in a suitable sense as well. Finally, we show that bilipschitz neural operators may always be written in the form of an alternating composition of strongly monotone neural operators, plus a simple isometry. Thus we realize a rigorous platform for discretization of a generalization of a neural operator. We also show that neural operators of this type may be approximated through the composition of finite-rank residual neural operators, where each block is strongly monotone, and may be inverted locally via iteration. We conclude by providing a quantitative approximation result for the discretization of general bilipschitz neural operators.

(Deep) Generative Geodesics

In this work, we propose to study the global geometrical properties of generative models. We introduce a new Riemannian metric to assess the similarity between any two data points. Importantly, our metric is agnostic to the parametrization of the generative model and requires only the evaluation of its data likelihood. Moreover, the metric leads to the conceptual definition of generative distances and generative geodesics, whose computation can be done efficiently in the data space. Their approximations are proven to converge to their true values under mild conditions. We showcase three proof-of-concept applications of this global metric, including clustering, data visualization, and data interpolation, thus providing new tools to support the geometrical understanding of generative models.

Globally injective and bijective neural operators

Recently there has been great interest in operator learning, where networks learn operators between function spaces from an essentially infinite-dimensional perspective. In this work we present results for when the operators learned by these networks are injective and surjective. As a warmup, we combine prior work in both the finite-dimensional ReLU and operator learning setting by giving sharp conditions under which ReLU layers with linear neural operators are injective. We then consider the case the case when the activation function is pointwise bijective and obtain sufficient conditions for the layer to be injective. We remark that this question, while trivial in the finite-rank case, is subtler in the infinite-rank case and is proved using tools from Fredholm theory. Next, we prove that our supplied injective neural operators are universal approximators and that their implementation, with finite-rank neural networks, are still injective. This ensures that injectivity is not `lost' in the transcription from analytical operators to their finite-rank implementation with networks. Finally, we conclude with an increase in abstraction and consider general conditions when subnetworks, which may be many layers deep, are injective and surjective and provide an exact inversion from a `linearization.' This section uses general arguments from Fredholm theory and Leray-Schauder degree theory for non-linear integral equations to analyze the mapping properties of neural operators in function spaces. These results apply to subnetworks formed from the layers considered in this work, under natural conditions. We believe that our work has applications in Bayesian UQ where injectivity enables likelihood estimation and in inverse problems where surjectivity and injectivity corresponds to existence and uniqueness, respectively.

Deep Invertible Approximation of Topologically Rich Maps between Manifolds

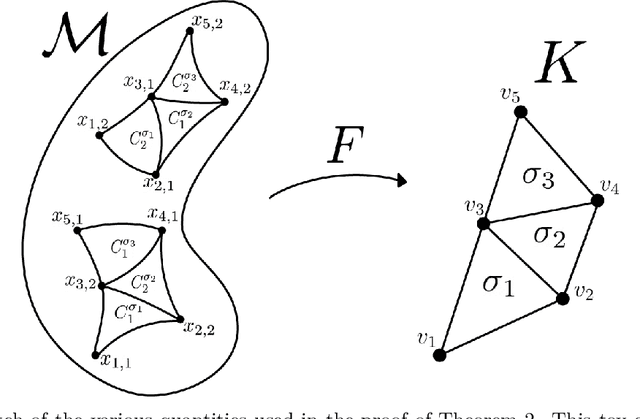
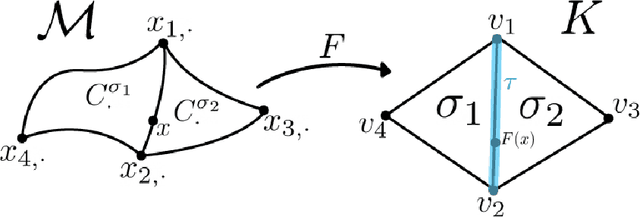
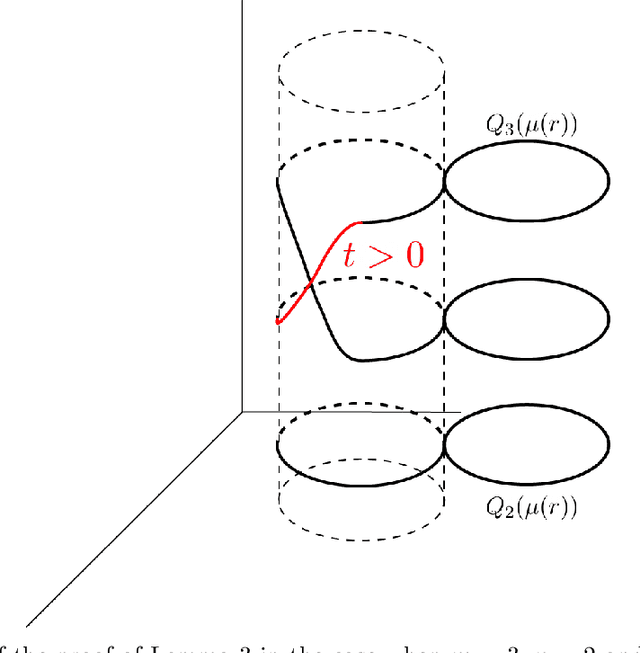
How can we design neural networks that allow for stable universal approximation of maps between topologically interesting manifolds? The answer is with a coordinate projection. Neural networks based on topological data analysis (TDA) use tools such as persistent homology to learn topological signatures of data and stabilize training but may not be universal approximators or have stable inverses. Other architectures universally approximate data distributions on submanifolds but only when the latter are given by a single chart, making them unable to learn maps that change topology. By exploiting the topological parallels between locally bilipschitz maps, covering spaces, and local homeomorphisms, and by using universal approximation arguments from machine learning, we find that a novel network of the form $\mathcal{T} \circ p \circ \mathcal{E}$, where $\mathcal{E}$ is an injective network, $p$ a fixed coordinate projection, and $\mathcal{T}$ a bijective network, is a universal approximator of local diffeomorphisms between compact smooth submanifolds embedded in $\mathbb{R}^n$. We emphasize the case when the target map changes topology. Further, we find that by constraining the projection $p$, multivalued inversions of our networks can be computed without sacrificing universality. As an application, we show that learning a group invariant function with unknown group action naturally reduces to the question of learning local diffeomorphisms for finite groups. Our theory permits us to recover orbits of the group action. We also outline possible extensions of our architecture to address molecular imaging of molecules with symmetries. Finally, our analysis informs the choice of topologically expressive starting spaces in generative problems.

Universal Joint Approximation of Manifolds and Densities by Simple Injective Flows

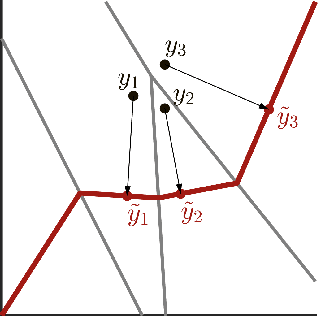
We analyze neural networks composed of bijective flows and injective expansive elements. We find that such networks universally approximate a large class of manifolds simultaneously with densities supported on them. Among others, our results apply to the well-known coupling and autoregressive flows. We build on the work of Teshima et al. 2020 on bijective flows and study injective architectures proposed in Brehmer et al. 2020 and Kothari et al. 2021. Our results leverage a new theoretical device called the embedding gap, which measures how far one continuous manifold is from embedding another. We relate the embedding gap to a relaxation of universally we call the manifold embedding property, capturing the geometric part of universality. Our proof also establishes that optimality of a network can be established in reverse, resolving a conjecture made in Brehmer et al. 2020 and opening the door for simple layer-wise training schemes. Finally, we show that the studied networks admit an exact layer-wise projection result, Bayesian uncertainty quantification, and black-box recovery of network weights.

Globally Injective ReLU Networks

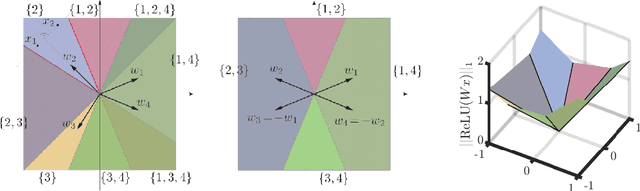
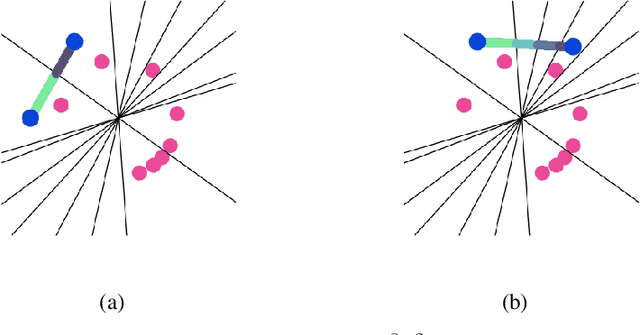
We study injective ReLU neural networks. Injectivity plays an important role in generative models where it facilitates inference; in inverse problems with generative priors it is a precursor to well posedness. We establish sharp conditions for injectivity of ReLU layers and networks, both fully connected and convolutional. We make no architectural assumptions beyond the ReLU activations so our results apply to a very general class of neural networks. We show through a layer-wise analysis that an expansivity factor of two is necessary for injectivity; we also show sufficiency by constructing weight matrices which guarantee injectivity. Further, we show that global injectivity with iid Gaussian matrices, a commonly used tractable model, requires considerably larger expansivity which might seem counterintuitive. We then derive the inverse Lipschitz constants and study the approximation-theoretic properties of injective neural networks. Using arguments from differential topology we prove that, under mild technical conditions, any Lipschitz map can be approximated by an injective neural network. This justifies the use of injective neural networks in problems which a priori do not require injectivity. Our results establish a theoretical basis for the study of nonlinear inverse and inference problems using neural networks.