Failure-Proof Non-Contrastive Self-Supervised Learning

We identify sufficient conditions to avoid known failure modes, including representation, dimensional, cluster and intracluster collapses, occurring in non-contrastive self-supervised learning. Based on these findings, we propose a principled design for the projector and loss function. We theoretically demonstrate that this design introduces an inductive bias that promotes learning representations that are both decorrelated and clustered without explicit enforcing these properties and leading to improved generalization. To the best of our knowledge, this is the first solution that achieves robust training with respect to these failure modes while guaranteeing enhanced generalization performance in downstream tasks. We validate our theoretical findings on image datasets including SVHN, CIFAR10, CIFAR100 and ImageNet-100, and show that our solution, dubbed FALCON, outperforms existing feature decorrelation and cluster-based self-supervised learning methods in terms of generalization to clustering and linear classification tasks.

EXPLAIN, AGREE, LEARN: Scaling Learning for Neural Probabilistic Logic

Neural probabilistic logic systems follow the neuro-symbolic (NeSy) paradigm by combining the perceptive and learning capabilities of neural networks with the robustness of probabilistic logic. Learning corresponds to likelihood optimization of the neural networks. However, to obtain the likelihood exactly, expensive probabilistic logic inference is required. To scale learning to more complex systems, we therefore propose to instead optimize a sampling based objective. We prove that the objective has a bounded error with respect to the likelihood, which vanishes when increasing the sample count. Furthermore, the error vanishes faster by exploiting a new concept of sample diversity. We then develop the EXPLAIN, AGREE, LEARN (EXAL) method that uses this objective. EXPLAIN samples explanations for the data. AGREE reweighs each explanation in concordance with the neural component. LEARN uses the reweighed explanations as a signal for learning. In contrast to previous NeSy methods, EXAL can scale to larger problem sizes while retaining theoretical guarantees on the error. Experimentally, our theoretical claims are verified and EXAL outperforms recent NeSy methods when scaling up the MNIST addition and Warcraft pathfinding problems.

(Deep) Generative Geodesics

In this work, we propose to study the global geometrical properties of generative models. We introduce a new Riemannian metric to assess the similarity between any two data points. Importantly, our metric is agnostic to the parametrization of the generative model and requires only the evaluation of its data likelihood. Moreover, the metric leads to the conceptual definition of generative distances and generative geodesics, whose computation can be done efficiently in the data space. Their approximations are proven to converge to their true values under mild conditions. We showcase three proof-of-concept applications of this global metric, including clustering, data visualization, and data interpolation, thus providing new tools to support the geometrical understanding of generative models.

A Bayesian Unification of Self-Supervised Clustering and Energy-Based Models

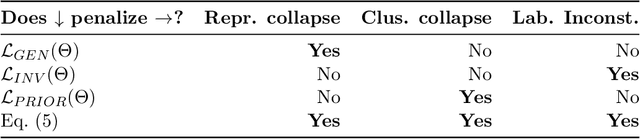
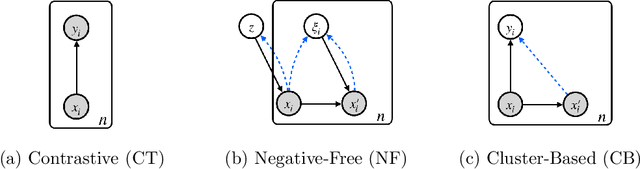
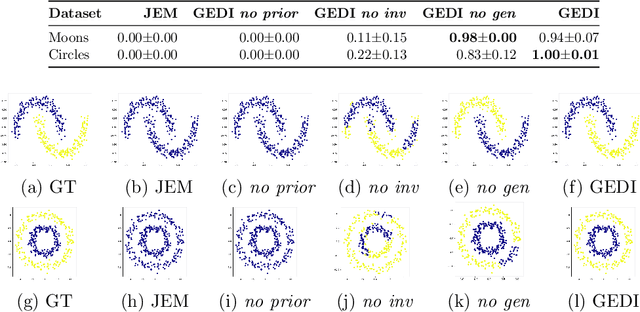
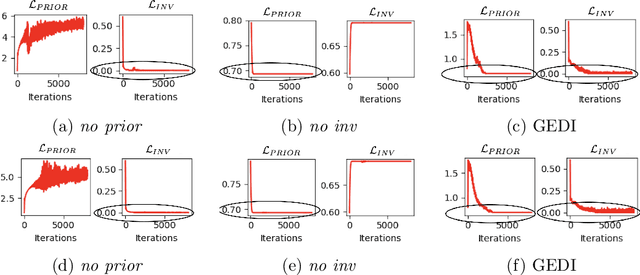
Self-supervised learning is a popular and powerful method for utilizing large amounts of unlabeled data, for which a wide variety of training objectives have been proposed in the literature. In this study, we perform a Bayesian analysis of state-of-the-art self-supervised learning objectives, elucidating the underlying probabilistic graphical models in each class and presenting a standardized methodology for their derivation from first principles. The analysis also indicates a natural means of integrating self-supervised learning with likelihood-based generative models. We instantiate this concept within the realm of cluster-based self-supervised learning and energy models, introducing a novel lower bound which is proven to reliably penalize the most important failure modes. Furthermore, this newly proposed lower bound enables the training of a standard backbone architecture without the necessity for asymmetric elements such as stop gradients, momentum encoders, or specialized clustering layers - typically introduced to avoid learning trivial solutions. Our theoretical findings are substantiated through experiments on synthetic and real-world data, including SVHN, CIFAR10, and CIFAR100, thus showing that our objective function allows to outperform existing self-supervised learning strategies in terms of clustering, generation and out-of-distribution detection performance by a wide margin. We also demonstrate that GEDI can be integrated into a neural-symbolic framework to mitigate the reasoning shortcut problem and to learn higher quality symbolic representations thanks to the enhanced classification performance.

Differentiable Sampling of Categorical Distributions Using the CatLog-Derivative Trick

Categorical random variables can faithfully represent the discrete and uncertain aspects of data as part of a discrete latent variable model. Learning in such models necessitates taking gradients with respect to the parameters of the categorical probability distributions, which is often intractable due to their combinatorial nature. A popular technique to estimate these otherwise intractable gradients is the Log-Derivative trick. This trick forms the basis of the well-known REINFORCE gradient estimator and its many extensions. While the Log-Derivative trick allows us to differentiate through samples drawn from categorical distributions, it does not take into account the discrete nature of the distribution itself. Our first contribution addresses this shortcoming by introducing the CatLog-Derivative trick - a variation of the Log-Derivative trick tailored towards categorical distributions. Secondly, we use the CatLog-Derivative trick to introduce IndeCateR, a novel and unbiased gradient estimator for the important case of products of independent categorical distributions with provably lower variance than REINFORCE. Thirdly, we empirically show that IndeCateR can be efficiently implemented and that its gradient estimates have significantly lower bias and variance for the same number of samples compared to the state of the art.

The Triad of Failure Modes and a Possible Way Out

We present a novel objective function for cluster-based self-supervised learning (SSL) that is designed to circumvent the triad of failure modes, namely representation collapse, cluster collapse, and the problem of invariance to permutations of cluster assignments. This objective consists of three key components: (i) A generative term that penalizes representation collapse, (ii) a term that promotes invariance to data augmentations, thereby addressing the issue of label permutations and (ii) a uniformity term that penalizes cluster collapse. Additionally, our proposed objective possesses two notable advantages. Firstly, it can be interpreted from a Bayesian perspective as a lower bound on the data log-likelihood. Secondly, it enables the training of a standard backbone architecture without the need for asymmetric elements like stop gradients, momentum encoders, or specialized clustering layers. Due to its simplicity and theoretical foundation, our proposed objective is well-suited for optimization. Experiments on both toy and real world data demonstrate its effectiveness

Learning Symbolic Representations Through Joint GEnerative and DIscriminative Training

We introduce GEDI, a Bayesian framework that combines existing self-supervised learning objectives with likelihood-based generative models. This framework leverages the benefits of both GEnerative and DIscriminative approaches, resulting in improved symbolic representations over standalone solutions. Additionally, GEDI can be easily integrated and trained jointly with existing neuro-symbolic frameworks without the need for additional supervision or costly pre-training steps. We demonstrate through experiments on real-world data, including SVHN, CIFAR10, and CIFAR100, that GEDI outperforms existing self-supervised learning strategies in terms of clustering performance by a significant margin. The symbolic component further allows it to leverage knowledge in the form of logical constraints to improve performance in the small data regime.

GEDI: GEnerative and DIscriminative Training for Self-Supervised Learning

Self-supervised learning is a popular and powerful method for utilizing large amounts of unlabeled data, for which a wide variety of training objectives have been proposed in the literature. In this study, we perform a Bayesian analysis of state-of-the-art self-supervised learning objectives and propose a unified formulation based on likelihood learning. Our analysis suggests a simple method for integrating self-supervised learning with generative models, allowing for the joint training of these two seemingly distinct approaches. We refer to this combined framework as GEDI, which stands for GEnerative and DIscriminative training. Additionally, we demonstrate an instantiation of the GEDI framework by integrating an energy-based model with a cluster-based self-supervised learning model. Through experiments on synthetic and real-world data, including SVHN, CIFAR10, and CIFAR100, we show that GEDI outperforms existing self-supervised learning strategies in terms of clustering performance by a wide margin. We also demonstrate that GEDI can be integrated into a neural-symbolic framework to address tasks in the small data regime, where it can use logical constraints to further improve clustering and classification performance.

VAEL: Bridging Variational Autoencoders and Probabilistic Logic Programming

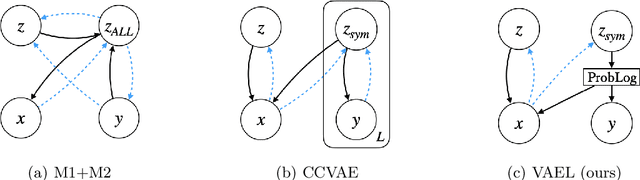
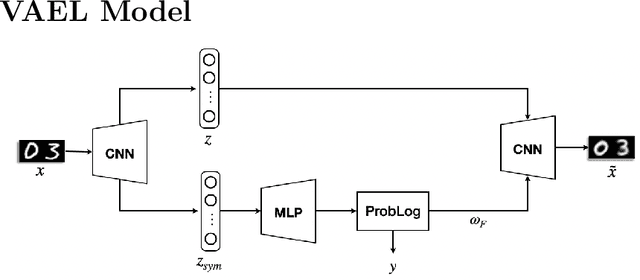
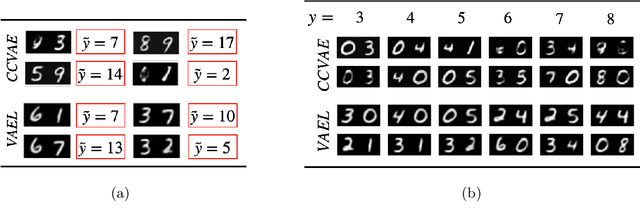
We present VAEL, a neuro-symbolic generative model integrating variational autoencoders (VAE) with the reasoning capabilities of probabilistic logic (L) programming. Besides standard latent subsymbolic variables, our model exploits a probabilistic logic program to define a further structured representation, which is used for logical reasoning. The entire process is end-to-end differentiable. Once trained, VAEL can solve new unseen generation tasks by (i) leveraging the previously acquired knowledge encoded in the neural component and (ii) exploiting new logical programs on the structured latent space. Our experiments provide support on the benefits of this neuro-symbolic integration both in terms of task generalization and data efficiency. To the best of our knowledge, this work is the first to propose a general-purpose end-to-end framework integrating probabilistic logic programming into a deep generative model.

LSB: Local Self-Balancing MCMC in Discrete Spaces

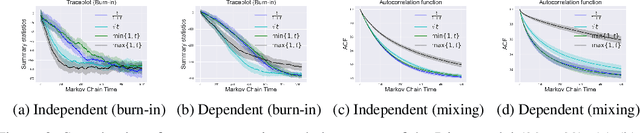
Markov Chain Monte Carlo (MCMC) methods are promising solutions to sample from target distributions in high dimensions. While MCMC methods enjoy nice theoretical properties, like guaranteed convergence and mixing to the true target, in practice their sampling efficiency depends on the choice of the proposal distribution and the target at hand. This work considers using machine learning to adapt the proposal distribution to the target, in order to improve the sampling efficiency in the purely discrete domain. Specifically, (i) it proposes a new parametrization for a family of proposal distributions, called locally balanced proposals, (ii) it defines an objective function based on mutual information and (iii) it devises a learning procedure to adapt the parameters of the proposal to the target, thus achieving fast convergence and fast mixing. We call the resulting sampler as the Locally Self-Balancing Sampler (LSB). We show through experimental analysis on the Ising model and Bayesian networks that LSB is indeed able to improve the efficiency over a state-of-the-art sampler based on locally balanced proposals, thus reducing the number of iterations required to converge, while achieving comparable mixing performance.