EXPLAIN, AGREE, LEARN: Scaling Learning for Neural Probabilistic Logic

Neural probabilistic logic systems follow the neuro-symbolic (NeSy) paradigm by combining the perceptive and learning capabilities of neural networks with the robustness of probabilistic logic. Learning corresponds to likelihood optimization of the neural networks. However, to obtain the likelihood exactly, expensive probabilistic logic inference is required. To scale learning to more complex systems, we therefore propose to instead optimize a sampling based objective. We prove that the objective has a bounded error with respect to the likelihood, which vanishes when increasing the sample count. Furthermore, the error vanishes faster by exploiting a new concept of sample diversity. We then develop the EXPLAIN, AGREE, LEARN (EXAL) method that uses this objective. EXPLAIN samples explanations for the data. AGREE reweighs each explanation in concordance with the neural component. LEARN uses the reweighed explanations as a signal for learning. In contrast to previous NeSy methods, EXAL can scale to larger problem sizes while retaining theoretical guarantees on the error. Experimentally, our theoretical claims are verified and EXAL outperforms recent NeSy methods when scaling up the MNIST addition and Warcraft pathfinding problems.

A Table-Based Representation for Probabilistic Logic: Preliminary Results

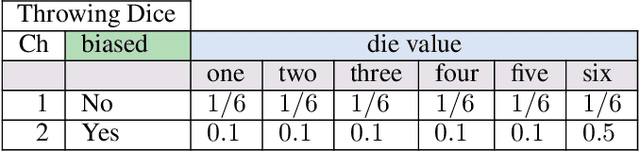
We present Probabilistic Decision Model and Notation (pDMN), a probabilistic extension of Decision Model and Notation (DMN). DMN is a modeling notation for deterministic decision logic, which intends to be user-friendly and low in complexity. pDMN extends DMN with probabilistic reasoning, predicates, functions, quantification, and a new hit policy. At the same time, it aims to retain DMN's user-friendliness to allow its usage by domain experts without the help of IT staff. pDMN models can be unambiguously translated into ProbLog programs to answer user queries. ProbLog is a probabilistic extension of Prolog flexibly enough to model and reason over any pDMN model.