Relational Neurosymbolic Markov Models

Sequential problems are ubiquitous in AI, such as in reinforcement learning or natural language processing. State-of-the-art deep sequential models, like transformers, excel in these settings but fail to guarantee the satisfaction of constraints necessary for trustworthy deployment. In contrast, neurosymbolic AI (NeSy) provides a sound formalism to enforce constraints in deep probabilistic models but scales exponentially on sequential problems. To overcome these limitations, we introduce relational neurosymbolic Markov models (NeSy-MMs), a new class of end-to-end differentiable sequential models that integrate and provably satisfy relational logical constraints. We propose a strategy for inference and learning that scales on sequential settings, and that combines approximate Bayesian inference, automated reasoning, and gradient estimation. Our experiments show that NeSy-MMs can solve problems beyond the current state-of-the-art in neurosymbolic AI and still provide strong guarantees with respect to desired properties. Moreover, we show that our models are more interpretable and that constraints can be adapted at test time to out-of-distribution scenarios.

A Fast Convoluted Story: Scaling Probabilistic Inference for Integer Arithmetic

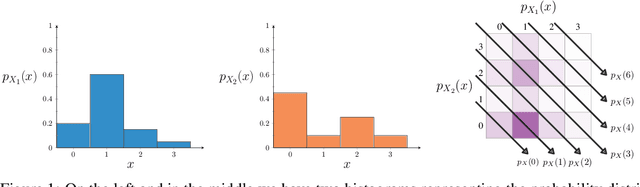
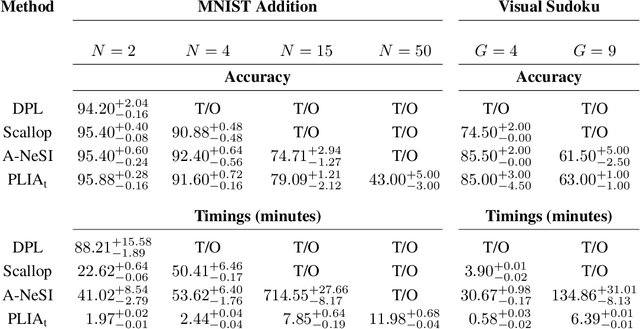
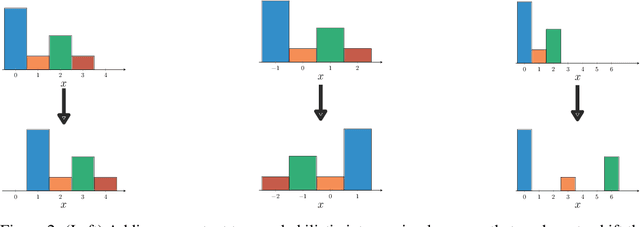
As illustrated by the success of integer linear programming, linear integer arithmetic is a powerful tool for modelling combinatorial problems. Furthermore, the probabilistic extension of linear programming has been used to formulate problems in neurosymbolic AI. However, two key problems persist that prevent the adoption of neurosymbolic techniques beyond toy problems. First, probabilistic inference is inherently hard, #P-hard to be precise. Second, the discrete nature of integers renders the construction of meaningful gradients challenging, which is problematic for learning. In order to mitigate these issues, we formulate linear arithmetic over integer-valued random variables as tensor manipulations that can be implemented in a straightforward fashion using modern deep learning libraries. At the core of our formulation lies the observation that the addition of two integer-valued random variables can be performed by adapting the fast Fourier transform to probabilities in the log-domain. By relying on tensor operations we obtain a differentiable data structure, which unlocks, virtually for free, gradient-based learning. In our experimental validation we show that tensorising probabilistic linear integer arithmetic and leveraging the fast Fourier transform allows us to push the state of the art by several orders of magnitude in terms of inference and learning times.

EXPLAIN, AGREE, LEARN: Scaling Learning for Neural Probabilistic Logic

Neural probabilistic logic systems follow the neuro-symbolic (NeSy) paradigm by combining the perceptive and learning capabilities of neural networks with the robustness of probabilistic logic. Learning corresponds to likelihood optimization of the neural networks. However, to obtain the likelihood exactly, expensive probabilistic logic inference is required. To scale learning to more complex systems, we therefore propose to instead optimize a sampling based objective. We prove that the objective has a bounded error with respect to the likelihood, which vanishes when increasing the sample count. Furthermore, the error vanishes faster by exploiting a new concept of sample diversity. We then develop the EXPLAIN, AGREE, LEARN (EXAL) method that uses this objective. EXPLAIN samples explanations for the data. AGREE reweighs each explanation in concordance with the neural component. LEARN uses the reweighed explanations as a signal for learning. In contrast to previous NeSy methods, EXAL can scale to larger problem sizes while retaining theoretical guarantees on the error. Experimentally, our theoretical claims are verified and EXAL outperforms recent NeSy methods when scaling up the MNIST addition and Warcraft pathfinding problems.

Differentiable Sampling of Categorical Distributions Using the CatLog-Derivative Trick

Categorical random variables can faithfully represent the discrete and uncertain aspects of data as part of a discrete latent variable model. Learning in such models necessitates taking gradients with respect to the parameters of the categorical probability distributions, which is often intractable due to their combinatorial nature. A popular technique to estimate these otherwise intractable gradients is the Log-Derivative trick. This trick forms the basis of the well-known REINFORCE gradient estimator and its many extensions. While the Log-Derivative trick allows us to differentiate through samples drawn from categorical distributions, it does not take into account the discrete nature of the distribution itself. Our first contribution addresses this shortcoming by introducing the CatLog-Derivative trick - a variation of the Log-Derivative trick tailored towards categorical distributions. Secondly, we use the CatLog-Derivative trick to introduce IndeCateR, a novel and unbiased gradient estimator for the important case of products of independent categorical distributions with provably lower variance than REINFORCE. Thirdly, we empirically show that IndeCateR can be efficiently implemented and that its gradient estimates have significantly lower bias and variance for the same number of samples compared to the state of the art.

Neural Probabilistic Logic Programming in Discrete-Continuous Domains

Neural-symbolic AI (NeSy) allows neural networks to exploit symbolic background knowledge in the form of logic. It has been shown to aid learning in the limited data regime and to facilitate inference on out-of-distribution data. Probabilistic NeSy focuses on integrating neural networks with both logic and probability theory, which additionally allows learning under uncertainty. A major limitation of current probabilistic NeSy systems, such as DeepProbLog, is their restriction to finite probability distributions, i.e., discrete random variables. In contrast, deep probabilistic programming (DPP) excels in modelling and optimising continuous probability distributions. Hence, we introduce DeepSeaProbLog, a neural probabilistic logic programming language that incorporates DPP techniques into NeSy. Doing so results in the support of inference and learning of both discrete and continuous probability distributions under logical constraints. Our main contributions are 1) the semantics of DeepSeaProbLog and its corresponding inference algorithm, 2) a proven asymptotically unbiased learning algorithm, and 3) a series of experiments that illustrate the versatility of our approach.